- ... CLASS="sans">ORAC .0.1
- The
ORAC program has been copyrighted (C) by Massimo Marchi and Piero
Procacci 1995-2008. This program is free software; you can
redistribute it and/or modify it under the terms of the GNU
General Public License as published by the Free Software
Foundation; either version 2 of the License, or (at your option) any
later version.
This program is distributed in the hope that it will be useful, but
WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
for more details. A general version of the GPL may be requested at: Free
Software Foundation, Inc., 59 Temple Place - Suite 330, Boston, MA
02111-1307, USA.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Procacci0.2
- Author to whom comments and bug reports
should be sent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... approximation1.1
- Of course SPME is itself an approximation
of the true electrostatic energy. This approximation is however totally
under control since the energy can be determined to any given accuracy and
the effect of finite accuracy can be easily controlled on any
computed property of the system. The approximation is
not uncontrolled.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bounds.1.2
- The explicit (i.e. atomistic) solvent
introduced in the MD cell is in fact the minimum amount required
such that the distance between any two portion of different
solute replicas is sufficiently large so as to assume negligible
interprotein interactions. Also the shape of the MD cell is usually
chosen so as to minimize the amount of explicit solvent whose sole
role, at an extremely demanding computational cost, is to provide
the correct dielectric medium for the biomolecule (including
microsolvation effects) .For example, globular
(i.e. quasi-spherical) proteins are usually simulated in a
dodecahedric box. Such a system, single solvated protein in PBC, is
thus representative of dilute solution of biomolecules since the
solute molecules in the periodic systems can never come close
to each other, thereby interacting
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
equations.2.1
- Symplectic means ``intertwined'' in Greek and
refers to the interlaced role of coordinate and momenta in
Hamilton's equations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... macro-step2.2
- When the large step
size at which the intermittent impulses are computed matches the
period of natural oscillations in the system, one can detect instabilities
of the numerical integration due to resonance effects. Resonances
occurs for pathological systems such as fast harmonic oscillators in
presence of strong, albeit slowly varying, forces [70]
and can be cured easily by tuning the time steps in the multilevel
integration. However, for large and complex molecules it is unlikely
that an artificial resonance could sustain for any length of
time [70]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... micro-steps.2.3
- In the original force breakup [19,20], the energy is not
generally conserved during the unperturbed motion of the inner
reference systems but only at the end of the
full macro-step. Force breakup and potential breakup have been
proved to produce identical trajectories [23]. With
respect to the force the breakup, implementation of the potential breakup is
slightly more complicated when dealing with intermolecular potential
separation, but the energy conservation requirement in any defined
reference system makes the debugging process easier.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... system.2.4
- For example, our conclusions on the
effect of SHAKE onto torsional motions for highly flexible systems
differs form the results published by Watanabe and Karplus
[82] for another flexible system. i.e. met-enkephalin in
vacuo. They compared SHAKE on
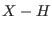 against full flexibility and
found that the power spectrum of torsional degrees of freedom differs
significantly. For met-enkephalin their spectrum, evaluated on a 10 ps
time span, shows a single strong peak at 10 or 40 wavenumbers,
with and without constraints, respectively. The different behavior of the
constrained and totally flexible system might be ascribed in their case
to the the specificity of the system and/or the potential, although
this seems unlikely [24]. In their study, on the other
hand, we must remark the unusual shape of the spectral torsional
profile with virtually no frequencies above 100 wavenumbers and with
strong peaks suspiciously close the minimum detectable frequency
according to their spectral resolution.
against full flexibility and
found that the power spectrum of torsional degrees of freedom differs
significantly. For met-enkephalin their spectrum, evaluated on a 10 ps
time span, shows a single strong peak at 10 or 40 wavenumbers,
with and without constraints, respectively. The different behavior of the
constrained and totally flexible system might be ascribed in their case
to the the specificity of the system and/or the potential, although
this seems unlikely [24]. In their study, on the other
hand, we must remark the unusual shape of the spectral torsional
profile with virtually no frequencies above 100 wavenumbers and with
strong peaks suspiciously close the minimum detectable frequency
according to their spectral resolution.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... PT3.1
- When P is not in boldface, we imply that the stress is
isotropic
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... groups3.2
- For large
molecules it may be convenient to further subdivide the molecule
into groups. A group, therefore encompasses a conveniently chosen subset
of the atoms of the molecule
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... respectively3.3
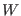 has actually the dimension of
a mass, while
has actually the dimension of
a mass, while 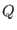 has the dimension of a mass time a length squared
has the dimension of a mass time a length squared
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline34340#�3.4
- This
allows to maintain Verlet-like
breakup while integrating the equation of motions [26].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as3.5
-
In presence of bond constraints and if the scaling is group-based
instead of molecular based, these expression should contain a
contribution from the constraints forces. Complications due to the
constraints can be avoided altogether by defining groups so that no
two groups are connected through a constrained bond [27]. In
that case
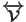 does not include any constraint contribution.
does not include any constraint contribution.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... barostat3.6
- The thermostat degree of freedom must
be included [86,91] in the count when working in virtual coordinates. Indeed in Eq. (3.13) we have
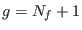
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....3.7
-
Actually in ref. [91,27] is pointed out that the
virial theorem implied by the distribution (3.33) is
slightly different from the exact virial in the NPT ensemble. Martyna
et al. [91] proposed an improved set of equations of
motion that generates a distribution satisfying exactly the virial
theorem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zero3.8
- The statement
the molecule of group does not dissociate is even too restrictive.
It is enough to say that the quantity (3.52) remains bound.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
term3.9
- Similar considerations hold for the thermostat
coordinate which in principle depends on the kinetic energy of all
degrees of freedom, modulated hence by the fast motion also. In this
case, however, the value of the thermostat inertia
parameter
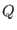 can be chosen to slow down the time scale of the
can be chosen to slow down the time scale of the
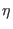 coordinates without reducing considerably the sampling
efficiency.
coordinates without reducing considerably the sampling
efficiency.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
integration.3.10
- There are also other less material reasons to
prefer molecular scaling: atomic scaling and molecular scaling yield
different dynamical properties because the equations of motions are
different. Dynamical data computed via extended system simulations
should always be taken with caution. With respect to pure Newtonian
dynamics, however, the
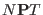 dynamical evolution is slightly
modified by a barostat coupled to the molecular center of
mass [26] but is brutally damaged when the barostat is
coupled to the fast degrees of freedom. For example in liquid flexible
nitrogen at normal pressure and 100 K, atomic scaling changes the
internal frequency by 20 cm
dynamical evolution is slightly
modified by a barostat coupled to the molecular center of
mass [26] but is brutally damaged when the barostat is
coupled to the fast degrees of freedom. For example in liquid flexible
nitrogen at normal pressure and 100 K, atomic scaling changes the
internal frequency by 20 cm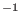 while no changes are detected when
the barostat is coupled to the centers of mass.
while no changes are detected when
the barostat is coupled to the centers of mass.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
infinity3.11
- The value of
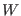 which works as ``infinity'' depends
on the ``force'' that is acting on barostat coordinate
expressed by the Eq. (3.25), i.e. on how far the system is
from the thermodynamic equilibrium. For a system near the thermodynamic
equilibrium with
which works as ``infinity'' depends
on the ``force'' that is acting on barostat coordinate
expressed by the Eq. (3.25), i.e. on how far the system is
from the thermodynamic equilibrium. For a system near the thermodynamic
equilibrium with
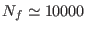 a value of
a value of 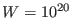 a.m.u. is
sufficient to prevent cell fluctuations.
a.m.u. is
sufficient to prevent cell fluctuations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... contacts4.1
- By excluded contacts we mean interactions
between charges on atoms connected by bonds or two bonds apart.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
as:4.2
- The scaled fractional coordinate is related to the scaled
coordinates in Eqs (3.1,3.34) by the relation
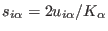 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...procacci954.3
- Here, the word group has a different
meaning that in Sec. 3 and stands for
sub ensemble of contiguous atoms
defined as having a total charge of approximately zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
interactions4.4
- Note that
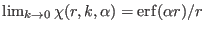 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....5.1
- In the latter equation
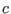 is a
constant that depends on the density of states of the
is a
constant that depends on the density of states of the 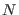 harmonic
oscillators and
harmonic
oscillators and
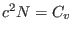 with
with 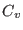 being the constant
volume heat capacity of the system.
being the constant
volume heat capacity of the system.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... solute.5.2
- With this definition,
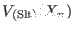 may
also depend on the coordinate of few solvent atoms. Being the
definition of the solute atom based rather than potential based, it
may be necessary to include in
may
also depend on the coordinate of few solvent atoms. Being the
definition of the solute atom based rather than potential based, it
may be necessary to include in
 , e.g.,
torsional terms that involve boundary solvent atoms.
, e.g.,
torsional terms that involve boundary solvent atoms.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... microstate6.1
- In Monte Carlo
generalized-ensemble simulations, momenta are dropped out.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline36468#�6.2
- Here, we assume implicitly that the indexes
 and
and  belong to an ordered list such that
belong to an ordered list such that
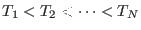 or
or
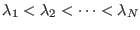 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as7.1
-
Lucy's function can be defined for a generic order
 such that it
has
such that it
has 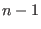 continuous derivative everywhere[139]. The
original definition[138] was given for
continuous derivative everywhere[139]. The
original definition[138] was given for 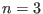 ; here it is
employed with
; here it is
employed with  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(PMF)8.1
- The potential of mean force is defined as
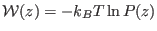 , where
, where
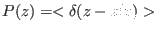 is the probability to find the system at the value of the reaction
coordinate
is the probability to find the system at the value of the reaction
coordinate
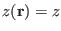 independently on all the other coordinates.
independently on all the other coordinates.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....8.2
- The Hamiltonian
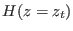 may
be imposed practically in steered molecular dynamics using
constraints or adding a stiff harmonic potential that keeps the
system at
may
be imposed practically in steered molecular dynamics using
constraints or adding a stiff harmonic potential that keeps the
system at 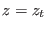 . Both these methods requires small corrections
when reconstructing the PMF. In particular, the use of constraints
on
. Both these methods requires small corrections
when reconstructing the PMF. In particular, the use of constraints
on 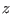 sets also
sets also 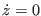 , a condition that is not present in the
definition of the PMF (see previous footnote). The correction to the PMF due this
extra artificial condition imposed through a generic constraint is
discussed in Ref. [147]. Stiff harmonic potentials, in the
sense that the associated stretching motion is decoupled from the
degrees of freedom of the system, behaves essentially like
constraints.[148] The depuration of the the PMF from the non
stiff harmonic driving potential in AFM experiments has bee
proposed bu Hummer and Szabo.[65]
, a condition that is not present in the
definition of the PMF (see previous footnote). The correction to the PMF due this
extra artificial condition imposed through a generic constraint is
discussed in Ref. [147]. Stiff harmonic potentials, in the
sense that the associated stretching motion is decoupled from the
degrees of freedom of the system, behaves essentially like
constraints.[148] The depuration of the the PMF from the non
stiff harmonic driving potential in AFM experiments has bee
proposed bu Hummer and Szabo.[65]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
bath8.3
- During the non equilibrium experiment, the instantaneous
``temperature'' of the system as measured by the kinetic energy may
well exceed that of the thermal bath. Actually the ``temperature''
cannot even be defined for a system that is not at equilibrium as
part of it, near the reaction path, can be warmer than other parts
that are far from the reaction coordinate. This has clearly no
consequences whatsoever on the CT, since the temperature in
Eq. 8.2 that of the system at the initial points which
are drawn by hypothesis at equilibrium
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...bennett768.4
- Bennett was the first
researcher to clearly recognize and formalize through the BAR the
superiority of bidirectional methods in the computation of free
energy differences. We cite verbatim form his
paper[118]: ``The best estimate of the free energy
difference is usually obtained by dividing the available computer
time approximately equally between the two ensembles; its efficiency
(variance x computer time) is never less, and may be several orders
of magnitude greater, than that obtained by sampling only one
ensemble, as is done in perturbation theory.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
9.1
- This last term does not contribute to the atomic forces but
only to the alchemical work and is constant for all non alchemical
species. The work done by an alchemical species through this term is
simply given by
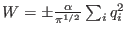 ,
depending whether the alchemical species has been charged or
discharged.
,
depending whether the alchemical species has been charged or
discharged.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.