Canonical Transformation and Symplectic Conditions
Given a system with  generalized coordinates
generalized coordinates 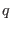 ,
,  conjugated
momenta
conjugated
momenta 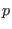 and Hamiltonian
and Hamiltonian 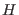 , the corresponding Hamilton's equations of
motion are
, the corresponding Hamilton's equations of
motion are
These equations can be written in a more compact form by defining a column
matrix with 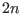 elements such that
elements such that
In this notation the Hamilton's equations (2.1)
can be compactly written as
where 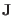 is a
is a
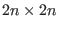 matrix,
matrix, 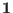 is an
is an 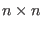 identity matrix and
identity matrix and 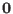 is a
is a 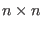 matrix of zeroes.
Eq. (2.3) is the so-called symplectic notation for the Hamilton's
equations.2.1
matrix of zeroes.
Eq. (2.3) is the so-called symplectic notation for the Hamilton's
equations.2.1
Using the same notation we now may define a transformation of
variables from
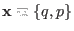 to
to
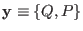 as
as
For a restricted canonical transformation [72,73]
we know that the function
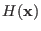 expressed in the new coordinates
expressed in the new coordinates 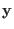 serves as the
Hamiltonian function for the new coordinates
serves as the
Hamiltonian function for the new coordinates 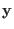 , that is the
Hamilton's equations of motion in the
, that is the
Hamilton's equations of motion in the 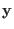 basis have exactly the same form
as in Eq. (2.3):
basis have exactly the same form
as in Eq. (2.3):
If we now take the time derivative of Eq. (2.4), use the
chain rule relating 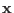 and
and 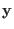 derivatives and use
Eq. (2.5), we arrive at
derivatives and use
Eq. (2.5), we arrive at
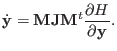 |
(2.6) |
Here 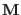 is the Jacobian matrix with elements
is the Jacobian matrix with elements
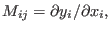 |
|
|
(2.7) |
and
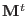 is its transpose.
By comparing Eqs. (2.5) and (2.6), we arrive at
the conclusion that a transformation is canonical if, and
only if, the Jacobian matrix
is its transpose.
By comparing Eqs. (2.5) and (2.6), we arrive at
the conclusion that a transformation is canonical if, and
only if, the Jacobian matrix 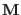 of the transformation
Eq. 2.4
satisfies the condition
of the transformation
Eq. 2.4
satisfies the condition
Eq. (2.8) is known as the symplectic condition for
canonical transformations and represents an effective tool to test
whether a generic transformation is canonical. Canonical
transformations play a key role in Hamiltonian dynamics.
For example, consider transformation 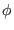
where
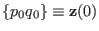 and
and
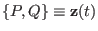 , i.e. one writes the coordinates and momenta at time
, i.e. one writes the coordinates and momenta at time 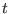 ,
obtained from the solution of the Hamiltonian equation of motion, as a function of the coordinates and momenta at the initial time
zero. This transformation, which depends on the scalar parameter
,
obtained from the solution of the Hamiltonian equation of motion, as a function of the coordinates and momenta at the initial time
zero. This transformation, which depends on the scalar parameter 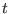 ,
is trivially canonical since both
,
is trivially canonical since both
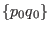 and
and 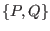 satisfies the Hamilton equations of motion. Hence the above
transformation defines the
satisfies the Hamilton equations of motion. Hence the above
transformation defines the 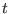 -flow mapping of the systems and, being
canonical, its Jacobian matrix obeys the symplectic condition
(2.8). An important consequence of the symplectic
condition, is the invariance under canonical (or symplectic)
transformations of many properties of the phase space. These invariant
properties are known as ``Poincare invariants'' or canonical
invariants. For example transformations or
-flow mapping of the systems and, being
canonical, its Jacobian matrix obeys the symplectic condition
(2.8). An important consequence of the symplectic
condition, is the invariance under canonical (or symplectic)
transformations of many properties of the phase space. These invariant
properties are known as ``Poincare invariants'' or canonical
invariants. For example transformations or 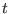 -flow's mapping obeying
Eq. (2.8) preserve the phase space volume. This is easy
to see, since the infinitesimal volume elements in the
-flow's mapping obeying
Eq. (2.8) preserve the phase space volume. This is easy
to see, since the infinitesimal volume elements in the 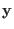 and
and
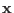 bases are related by
bases are related by
 |
|
|
(2.10) |
where
 is the Jacobian of the
transformation. Taking the determinant of the symplectic condition
Eq. (2.8) we see that
is the Jacobian of the
transformation. Taking the determinant of the symplectic condition
Eq. (2.8) we see that
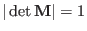 and therefore
and therefore
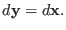 |
|
|
(2.11) |
For a canonical or symplectic 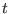 -flow mapping this means that
the phase total space volume is invariant and therefore Liouville
theorem is automatically satisfied.
-flow mapping this means that
the phase total space volume is invariant and therefore Liouville
theorem is automatically satisfied.
A step-wise numerical integration scheme defines a 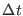 -flow mapping
or equivalently a coordinates transformation, that
is
-flow mapping
or equivalently a coordinates transformation, that
is
We have seen that exact solution of the Hamilton equations
has 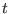 -flow mapping satisfying the symplectic conditions
(2.8). If the Jacobian matrix of the transformation
(2.12) satisfies the symplectic condition then
the integrator is termed to be symplectic.
The resulting integrator, therefore, exhibits properties identical
to those of the exact solution, in particular it satisfies Eq.
(2.11). Symplectic algorithms have also been proved to
be robust, i.e resistant to time step increase, and generate stable
long time trajectory, i.e. they do not show drifts of the total energy.
Popular MD algorithms like Verlet,
leap frog and velocity Verlet
are all symplectic and their robustness is now understood to
be due in part to this property.
[70,20,23,71]
-flow mapping satisfying the symplectic conditions
(2.8). If the Jacobian matrix of the transformation
(2.12) satisfies the symplectic condition then
the integrator is termed to be symplectic.
The resulting integrator, therefore, exhibits properties identical
to those of the exact solution, in particular it satisfies Eq.
(2.11). Symplectic algorithms have also been proved to
be robust, i.e resistant to time step increase, and generate stable
long time trajectory, i.e. they do not show drifts of the total energy.
Popular MD algorithms like Verlet,
leap frog and velocity Verlet
are all symplectic and their robustness is now understood to
be due in part to this property.
[70,20,23,71]
procacci
2021-12-29
![]() generalized coordinates
generalized coordinates ![]() ,
, ![]() conjugated
momenta
conjugated
momenta ![]() and Hamiltonian
and Hamiltonian ![]() , the corresponding Hamilton's equations of
motion are
, the corresponding Hamilton's equations of
motion are
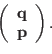
![]() to
to
![]() as
as
![]() -flow mapping
or equivalently a coordinates transformation, that
is
-flow mapping
or equivalently a coordinates transformation, that
is