Liouville Formalism: a Tool for Building Symplectic and
Reversible Integrators
In the previous paragraphs we have seen that it is highly beneficial for
an integrator to be symplectic. We may now wonder if there exists a
general way for obtaining symplectic and possibly, reversible
integrators from ``first principles''. To this end, we start by noting
that for any property which depends on time implicitly through
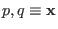 we have
we have
where the sum is extended to all  degrees of freedom in the
system.
degrees of freedom in the
system. 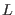 is the Liouvillean operator defined by
is the Liouvillean operator defined by
Eq. (2.13) can be integrated to yield
If 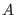 is the state vector itself we can use Eq. (2.15)
to integrate Hamilton's equations:
is the state vector itself we can use Eq. (2.15)
to integrate Hamilton's equations:
The above equation is a formal solution of Hamilton's equations of
motion. The exponential operator 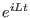 times the state vector
defines the t-flow of the
Hamiltonian system which brings the system phase space point from the initial
state
times the state vector
defines the t-flow of the
Hamiltonian system which brings the system phase space point from the initial
state
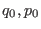 to the state
to the state 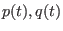 at a later time
at a later time 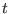 . We
already know that this transformation obeys Eq. (2.8). We may also
note that the adjoint of the exponential operator corresponds to the inverse, that
is
. We
already know that this transformation obeys Eq. (2.8). We may also
note that the adjoint of the exponential operator corresponds to the inverse, that
is 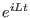 is unitary. This implies that the trajectory
is exactly time reversible. In order to build our integrator,
we now define the discrete time propagator
is unitary. This implies that the trajectory
is exactly time reversible. In order to build our integrator,
we now define the discrete time propagator
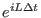 as
as
In principle, to evaluate the action of
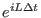 on the state vector
on the state vector 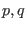 one should know the derivatives of all orders of the
potential
one should know the derivatives of all orders of the
potential 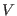 . This can be easily seen by Taylor expanding the discrete time
propagator
. This can be easily seen by Taylor expanding the discrete time
propagator
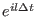 and noting that the operator
and noting that the operator
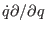 does not commute with
does not commute with
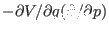 when the
coordinates and momenta refer to same degree of freedom.
We seek therefore approximate expressions of the discrete time propagator
that retain both the symplectic and the reversibility property.
For any two linear operators
when the
coordinates and momenta refer to same degree of freedom.
We seek therefore approximate expressions of the discrete time propagator
that retain both the symplectic and the reversibility property.
For any two linear operators 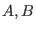 the Trotter formula [74]
holds:
the Trotter formula [74]
holds:
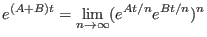 |
|
|
(2.19) |
We recognize that the propagator Eq. (2.18) has the
same structure as the left hand side of Eq. (2.19); hence,
using Eq. (2.19), we may write for 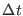 sufficiently
small
sufficiently
small
Where, for simplicity of discussion, we have omitted the sum over 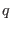 and
and 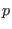 in the exponential.
Eq. (2.20) is exact in the limit that
in the exponential.
Eq. (2.20) is exact in the limit that
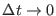 and
is first order for finite step size. Using Eq. (2.8) it is
easy to show that the t-flow defined in Eq. (2.20) is
symplectic, being the product of two successive symplectic transformations.
Unfortunately, the propagator Eq. (2.20) is not unitary and therefore
the corresponding algorithm is not time reversible. Again the non
unitarity is due to the fact that the two factorized exponential operators
are non commuting.
We can overcome this problem by halving the time step and
using the approximant:
and
is first order for finite step size. Using Eq. (2.8) it is
easy to show that the t-flow defined in Eq. (2.20) is
symplectic, being the product of two successive symplectic transformations.
Unfortunately, the propagator Eq. (2.20) is not unitary and therefore
the corresponding algorithm is not time reversible. Again the non
unitarity is due to the fact that the two factorized exponential operators
are non commuting.
We can overcome this problem by halving the time step and
using the approximant:
The resulting propagator is clearly unitary, therefore time
reversible, and is also correct to the second order
[75]. Thus, requiring that the product of the
exponential operator be unitary, automatically leads to more
accurate approximations of the true discrete time
propagator [76,75]. Applying
the same argument to the propagator (2.18) we have
The action of an exponential operator
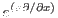 on a generic function
on a generic function 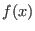 trivially corresponds to the Taylor expansion
of
trivially corresponds to the Taylor expansion
of 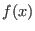 around the point
around the point 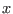 at the point
at the point 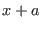 , that is
, that is
Using Eq. (2.23), the time reversible and symplectic
integration algorithm can now be derived by acting with our Hermitian
operator Eq. (2.22) onto the state vector at 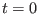 to
produce updated coordinate and momenta at a later time
to
produce updated coordinate and momenta at a later time 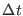 .
The resulting algorithm is completely equivalent to the well
known velocity Verlet:
.
The resulting algorithm is completely equivalent to the well
known velocity Verlet:
We first notice that each of the three transformations obeys the
symplectic condition Eq.
(2.8) and has a Jacobian determinant equal to one.
The product of the three transformation is also
symplectic and, thus, phase volume preserving. Finally, since the
discrete time propagator (2.22) is unitary,
the algorithm is time reversible.
One may wonder what it is obtained if the operators
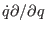 and
and
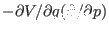 are exchanged in
the definition of the discrete time propagator (2.22). If we
do so, the new integrator is
are exchanged in
the definition of the discrete time propagator (2.22). If we
do so, the new integrator is
This algorithm has been proved to be equivalent to the so-called Leap-frog
algorithm [77]. Tuckerman et al. [20]
called this algorithm position Verlet which is certainly a
more appropriate name in the light of the exchanged role of positions and
velocities with respect to the velocity Verlet. Also, Eq. (2.21)
clearly shows that the position Verlet is essentially identical to the
Velocity Verlet. A shift of a time origin by
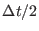 of either
Eq. (2.25) or Eq. (2.24) would actually make both
integrator perfectly equivalent. However, as pointed out in Ref. [21],
half time steps are not formally defined, being the right hand side of
Eq. (2.21)
an approximation of the discrete time propagator for the full step
of either
Eq. (2.25) or Eq. (2.24) would actually make both
integrator perfectly equivalent. However, as pointed out in Ref. [21],
half time steps are not formally defined, being the right hand side of
Eq. (2.21)
an approximation of the discrete time propagator for the full step
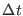 . Velocity Verlet and Position Verlet, therefore, do not generate
numerically identical trajectories although of course the trajectories are similar.
. Velocity Verlet and Position Verlet, therefore, do not generate
numerically identical trajectories although of course the trajectories are similar.
We conclude this section by saying that is indeed noticeable
that using the same Liouville formalism different long-time known schemes
can be derived. The Liouville approach represent therefore a unifying
treatment for understanding the properties and relationships between
stepwise integrators.
procacci
2021-12-29
![]() and
and
![]() are exchanged in
the definition of the discrete time propagator (2.22). If we
do so, the new integrator is
are exchanged in
the definition of the discrete time propagator (2.22). If we
do so, the new integrator is