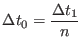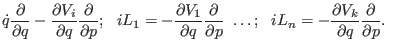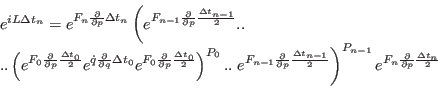Potential Subdivision and Multiple Time Steps
Integrators for NVE Simulations
The ideas developed in the preceding sections can be used
to build multiple time step integrators. Multiple time step
integration is based on the concept of reference system.
Let us now assume that the system potential 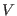 be subdivided in
be subdivided in
 terms such that
terms such that
Additionally, we suppose that
the corresponding average values of the square modulus of the forces
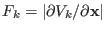 and of their time derivatives
and of their time derivatives
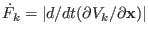 satisfy the
following condition:
satisfy the
following condition:
These equations express the situation where different time scales of
the system correspond to different pieces of the potential.
Thus, the Hamiltonian of the 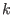 -th reference system is defined as
-th reference system is defined as
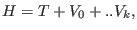 |
|
|
(2.28) |
with a perturbation given by:
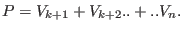 |
|
|
(2.29) |
For a general subdivision of the kind given in Eq. (2.26) there
exist  reference nested systems. In the general case of a
flexible molecular
systems, we have fast degrees of freedom which are governed by the
stretching, bending and torsional potentials and by slow intermolecular
motions driven by the intermolecular potential. As we shall discuss
with greater detail in section 4, in real systems there is
no clear cut condition between intra and intermolecular motions since their time
scales may well overlap in many cases. The conditions
Eq. (2.27) are, hence, never fully met for any of all
possible potential subdivisions.
reference nested systems. In the general case of a
flexible molecular
systems, we have fast degrees of freedom which are governed by the
stretching, bending and torsional potentials and by slow intermolecular
motions driven by the intermolecular potential. As we shall discuss
with greater detail in section 4, in real systems there is
no clear cut condition between intra and intermolecular motions since their time
scales may well overlap in many cases. The conditions
Eq. (2.27) are, hence, never fully met for any of all
possible potential subdivisions.
Given a potential subdivision Eq. (2.26),
we now show how a multi-step scheme can be built with the methods
described in section 2.2.
For the sake of simplicity, we
subdivide the interaction potential of a
molecular system into two components only: One intra molecular,
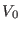 , generating mostly ``fast'' motions and the other
intermolecular,
, generating mostly ``fast'' motions and the other
intermolecular, 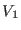 , driving slower degrees of
freedom. Generalization of the forthcoming discussion to a
, driving slower degrees of
freedom. Generalization of the forthcoming discussion to a  -fold
subdivision, Eq. (2.26), is then straightforward.
-fold
subdivision, Eq. (2.26), is then straightforward.
For the 2-fold inter/intra subdivision, the system with Hamiltonian
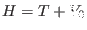 is called the intra-molecular reference system whereas
is called the intra-molecular reference system whereas
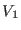 is the intermolecular perturbation to the reference
system. Correspondingly, the Liouvillean may be split as
is the intermolecular perturbation to the reference
system. Correspondingly, the Liouvillean may be split as
Here 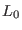 is the Liouvillean of the 0-th reference system with
Hamiltonian
is the Liouvillean of the 0-th reference system with
Hamiltonian 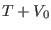 , while
, while 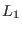 is a perturbation Liouvillean.
Let us now suppose now that
is a perturbation Liouvillean.
Let us now suppose now that
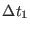 is a good time
discretization for the
time evolution of the perturbation, that is for the slowly varying
intermolecular
potential. The discrete
is a good time
discretization for the
time evolution of the perturbation, that is for the slowly varying
intermolecular
potential. The discrete
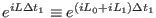 time propagator can be factorized as
time propagator can be factorized as
where we have used Eq. (2.21) and we have defined
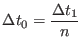 |
(2.32) |
as the time step for the ``fast'' reference system with Hamiltonian 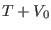 . The propagator (2.31) is unitary and hence
time reversible. The external propagators depending on the
Liouvillean
. The propagator (2.31) is unitary and hence
time reversible. The external propagators depending on the
Liouvillean 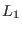 acting on the state vectors define a symplectic
mapping, as it can be easily proved by using Eq. (2.8). The
full factorized propagator is therefore symplectic as long as the
inner propagator is symplectic. The Liouvillean
acting on the state vectors define a symplectic
mapping, as it can be easily proved by using Eq. (2.8). The
full factorized propagator is therefore symplectic as long as the
inner propagator is symplectic. The Liouvillean
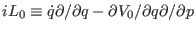 can be factorized
according to the Verlet symplectic and reversible breakup described in
the preceding section, but
with an Hamiltonian
can be factorized
according to the Verlet symplectic and reversible breakup described in
the preceding section, but
with an Hamiltonian 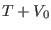 . Inserting the result into Eq. (2.31)
and using the definition (2.30), the resulting double time step
propagator is then
. Inserting the result into Eq. (2.31)
and using the definition (2.30), the resulting double time step
propagator is then
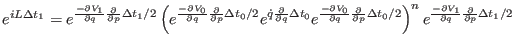 |
(2.33) |
This propagator is unfolded straightforwardly using the rule (2.23)
generating the following symplectic and reversible integrator from
step 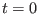 to
to
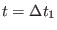 :
:
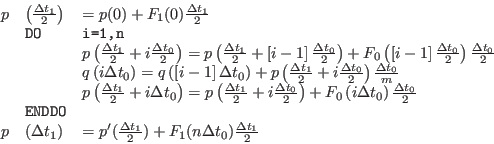 |
|
|
(2.34) |
Note that the slowly varying forces 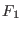 are felt only at the
beginning and the end of the macro-step2.2
are felt only at the
beginning and the end of the macro-step2.2
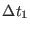 . In the inner
. In the inner  steps loop
the system moves only according to the Hamiltonian of the reference
system
steps loop
the system moves only according to the Hamiltonian of the reference
system
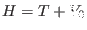 . When using the potential breakup, the inner
reference system is rigorously conservative and the total energy of the
reference system (i.e.
. When using the potential breakup, the inner
reference system is rigorously conservative and the total energy of the
reference system (i.e.
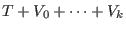 ) is
conserved during the
) is
conserved during the  micro-steps.2.3
micro-steps.2.3
The integration
algorithm given an arbitrary subdivision of the interaction potential
is now straightforward. For the general subdivision (2.26)
the corresponding Liouvillean split is
We write the discrete time operator for the Liouville operator
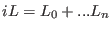 and use repeatedly the Hermitian approximant and Trotter formula
to get a hierarchy of nested reference systems propagator, viz.
and use repeatedly the Hermitian approximant and Trotter formula
to get a hierarchy of nested reference systems propagator, viz.
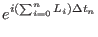 |
 |
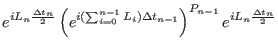 |
(2.36) |
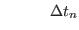 |
 |
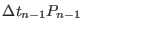 |
|
 |
 |
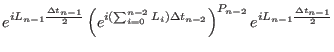 |
(2.37) |
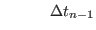 |
 |
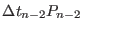 |
|
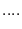 |
|
|
|
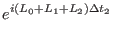 |
 |
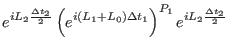 |
(2.38) |
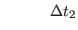 |
 |
 |
|
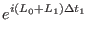 |
 |
 |
(2.39) |
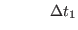 |
 |
 |
|
where
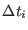 is the generic integration time steps selected according
to the time scale of the
is the generic integration time steps selected according
to the time scale of the 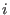 -th force
-th force 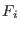 .
We now substitute Eq. (2.39) into Eq. (2.38)
and so on climbing the whole
hierarchy until Eq. (2.36). The resulting multiple time steps symplectic
and reversible propagator is then
.
We now substitute Eq. (2.39) into Eq. (2.38)
and so on climbing the whole
hierarchy until Eq. (2.36). The resulting multiple time steps symplectic
and reversible propagator is then
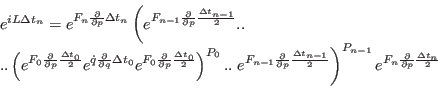 |
|
|
(2.40) |
The integration algorithm that can be derived from the above
propagator was first proposed by Tuckerman, Martyna and Berne and
called r-RESPA, reversible reference system propagation
algorithm [20]
procacci
2021-12-29
![]() , generating mostly ``fast'' motions and the other
intermolecular,
, generating mostly ``fast'' motions and the other
intermolecular, ![]() , driving slower degrees of
freedom. Generalization of the forthcoming discussion to a
, driving slower degrees of
freedom. Generalization of the forthcoming discussion to a ![]() -fold
subdivision, Eq. (2.26), is then straightforward.
-fold
subdivision, Eq. (2.26), is then straightforward.
![]() is called the intra-molecular reference system whereas
is called the intra-molecular reference system whereas
![]() is the intermolecular perturbation to the reference
system. Correspondingly, the Liouvillean may be split as
is the intermolecular perturbation to the reference
system. Correspondingly, the Liouvillean may be split as