Equivalence of Atomic and Molecular Pressure
The volume scaling defined in Eq. (3.1) is not unique.
Note that only the equation of motion for
the center of mass momentum, Eq. (3.25),
has a velocity dependent term that
depends on the coordinates of the barostat through the matrix 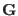 defined in Eq. (3.11). The atomic momenta, Eq. (3.24),
on the contrary, are not coupled to the barostat. This fact is also
reflected in
the equations of motion for the barostat momenta, Eq. (3.26), which is
driven by the internal pressure due only to the molecular or group
center of masses. In defining the extended Lagrangian
one could as well have defined an atomic scaling of the form
defined in Eq. (3.11). The atomic momenta, Eq. (3.24),
on the contrary, are not coupled to the barostat. This fact is also
reflected in
the equations of motion for the barostat momenta, Eq. (3.26), which is
driven by the internal pressure due only to the molecular or group
center of masses. In defining the extended Lagrangian
one could as well have defined an atomic scaling of the form
Atomic scaling might be trivially implemented by eliminating
the kinetic energy, which depends on the
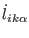 velocities,
from the starting Lagrangian (3.6) and replacing
the term
velocities,
from the starting Lagrangian (3.6) and replacing
the term
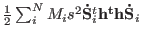 with
with
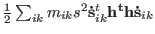 .
The corresponding equations of motions for atomic scaling are then
.
The corresponding equations of motions for atomic scaling are then
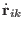 |
 |
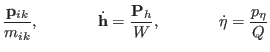 |
(3.34) |
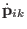 |
 |
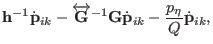 |
(3.35) |
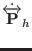 |
 |
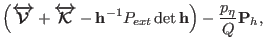 |
(3.36) |
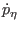 |
 |
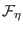 |
(3.37) |
where the quantities
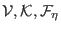 depend now on the atomic coordinates
depend now on the atomic coordinates
In case of atomic, Eq. (3.34),
or molecular scaling, Eq. (3.1), the internal pressure
entering in Eqs. (3.26,3.37) is then
respectively.
Where the molecular quantities can be written in term of the atomic
counterpart according to:
The equation of motion for the barostat in the two cases,
Eqs.(3.37, 3.26), has the same form whether atomic or
molecular scaling is adopted. The internal pressure in the former case
is given by Eq. (3.41) and in the latter is given by
Eq. (3.42). The two pressures,
Eqs. (3.41,3.42), differ
instantaneously. Should the difference persist after averaging, then
it would be obvious that the equilibrium thermodynamic state in the
 ensemble depends on the scaling method. The two formulas
(3.41,3.42) are fortunately equivalent. To
prove this statement, we closely follow the route proposed by
H. Berendsen and reported by Ciccotti and Ryckaert [98] and use
Eqs. (3.43-3.45) to rearrange Eq.
(3.42). We obtain
ensemble depends on the scaling method. The two formulas
(3.41,3.42) are fortunately equivalent. To
prove this statement, we closely follow the route proposed by
H. Berendsen and reported by Ciccotti and Ryckaert [98] and use
Eqs. (3.43-3.45) to rearrange Eq.
(3.42). We obtain
Adding and subtracting
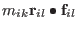 ,
we get
,
we get
| |
 |
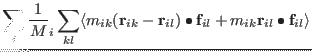 |
(3.46) |
which can be rearranged as
| |
 |
![$\displaystyle \sum_i {1 \over M_i}
\left\{
\sum_{ kl }
\left[
{1 \over 2}
\lang...
...
\right ] +
\sum_l
\langle
{\bf r}_{ il } \bullet {\bf f}_{il}
\rangle
\right\}$](img358.png) |
(3.47) |
using the newton law
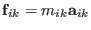 , where
, where
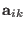 is the acceleration, we obtain
is the acceleration, we obtain
| |
 |
![$\displaystyle \sum_i {1 \over M_i} \left \{ \sum_{ kl }
\left[
{1 \over 2}
\lan...
...ght ]
+ \sum_l \langle {\bf r}_{ il } \bullet {\bf f}_{ il } \rangle \right \}.$](img361.png) |
(3.48) |
The first term in the above equation can be decomposed according to:
The first derivative term on the right hand side is zero rigorously
for rigid molecules or rigid group
and is zero on average for flexible molecules or groups,
assuming that the flexible molecules or groups do not dissociate.
This can be readily seen in case of
ergodic systems, by evaluating directly the average of this derivatives as
| |
 |
![$\displaystyle \lim_{\tau \rightarrow \infty} {1 \over \tau} \left [
({\bf r}_{ ...
...l }(\tau )) \bullet
({\bf v}_{ il }(\tau) - {\bf v}_{ ik } (\tau)) + C \right ]$](img366.png) |
(3.51) |
So if the quantity
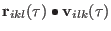 remains bounded
(which is true if the potential is not dissociative, since
remains bounded
(which is true if the potential is not dissociative, since 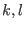 refers to the same
molecule
refers to the same
molecule 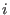 ), the average in Eq. (3.52) is zero3.8.
Thus, we can rewrite the average of Eq. (3.49) as
), the average in Eq. (3.52) is zero3.8.
Thus, we can rewrite the average of Eq. (3.49) as
The first term on the right hand side of the above equation can be
further developed obtaining the trivial identity:
Substituting Eq. (3.55) in Eq. (3.53) we
get
Substituting Eq. (3.56) into Eq. (3.42) leads
speedily to (3.41) which completes the proof.
As a consequence of the above discussion, it seems likely that both
the equilibrium and non equilibrium properties of the MD system are
not affected by coordinate scaling. We shall see later that this is
actually the case.
procacci
2021-12-29
![]() ensemble depends on the scaling method. The two formulas
(3.41,3.42) are fortunately equivalent. To
prove this statement, we closely follow the route proposed by
H. Berendsen and reported by Ciccotti and Ryckaert [98] and use
Eqs. (3.43-3.45) to rearrange Eq.
(3.42). We obtain
ensemble depends on the scaling method. The two formulas
(3.41,3.42) are fortunately equivalent. To
prove this statement, we closely follow the route proposed by
H. Berendsen and reported by Ciccotti and Ryckaert [98] and use
Eqs. (3.43-3.45) to rearrange Eq.
(3.42). We obtain
![$\displaystyle \langle
{ d \over { dt } }
\left[
({\bf r}_{ ik } - {\bf r}_{ il } ) \bullet
({\bf v}_{ il } - {\bf v}_{ ik } )
\right] \rangle$](img364.png)
![$\displaystyle \lim_{\tau \rightarrow \infty} {1 \over \tau} \int_{0}^{\infty}
{...
...{ ik } - {\bf r}_{ il } ) \bullet
({\bf v}_{ il } - {\bf v}_{ ik } )
\right] dt$](img365.png)