We have seen in section 2.2 that the knowledge of the Liouvillean
allows us to straightforwardly derive a multi-step integration algorithm.
Thus, for simulation in the 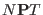 ensemble, the Liouvillean
ensemble, the Liouvillean
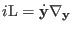 is readily available from the equations of motion
in (3.23-3.27). For sake of simplicity, to build our
is readily available from the equations of motion
in (3.23-3.27). For sake of simplicity, to build our
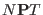 multiple time step integrator we
assume that the system potential contains only a fast
intramolecular
multiple time step integrator we
assume that the system potential contains only a fast
intramolecular 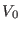 term and a slow intermolecular
term
term and a slow intermolecular
term 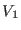 , as discussed in Sec. 2.3. Generalization
to multiple intra and inter-molecular
components is straightforward.
, as discussed in Sec. 2.3. Generalization
to multiple intra and inter-molecular
components is straightforward.
We define the following components of the
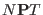 Liouvillean
Liouvillean
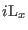 |
 |
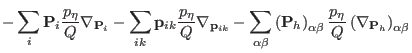 |
(3.56) |
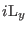 |
 |
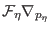 |
(3.57) |
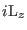 |
 |
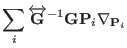 |
(3.58) |
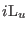 |
 |
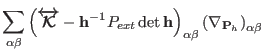 |
(3.59) |
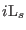 |
 |
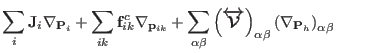 |
(3.60) |
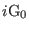 |
 |
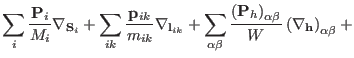 |
|
| |
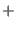 |
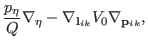 |
(3.61) |
where in Eq. (3.61) the scaled forces
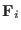 have been replaced
by its real space counterparts, i.e.
have been replaced
by its real space counterparts, i.e.
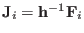 .
.
The atomic scaling version of this Liouvillean breakup is derived on the basis
of Eqs. (3.38). One obtains
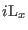 |
 |
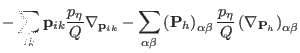 |
(3.62) |
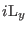 |
 |
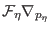 |
(3.63) |
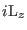 |
 |
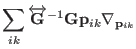 |
(3.64) |
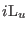 |
 |
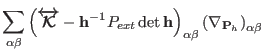 |
(3.65) |
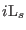 |
 |
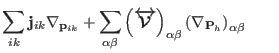 |
(3.66) |
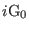 |
 |
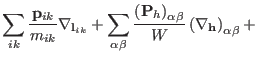 |
|
| |
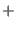 |
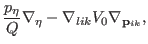 |
(3.67) |
where
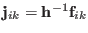 and
and
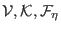 are given in
Eqs. (3.39,3.40). For the time scale breakup in
the
are given in
Eqs. (3.39,3.40). For the time scale breakup in
the
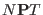 ensemble we have the complication of the extra
degrees of freedom whose time scale dynamics can be controlled by
varying the parameter
ensemble we have the complication of the extra
degrees of freedom whose time scale dynamics can be controlled by
varying the parameter 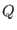 and
and 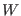 . Large values of
. Large values of 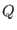 and
and 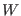 slow
down the time dynamics of the barostat and thermostat coordinates.
The potential
slow
down the time dynamics of the barostat and thermostat coordinates.
The potential 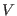 determines the time scale of the
determines the time scale of the 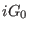 term (the
fast component) and of the
term (the
fast component) and of the 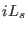 contribution (the slow
component). All other sub-Liouvilleans either handle the coupling of
the true coordinates to the extra degrees of freedom (
contribution (the slow
component). All other sub-Liouvilleans either handle the coupling of
the true coordinates to the extra degrees of freedom (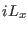 expresses the coupling of all momenta (including barostat
momenta) to the thermostat momentum, while
expresses the coupling of all momenta (including barostat
momenta) to the thermostat momentum, while 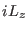 is a coupling
term between the center of mass momenta and the barostat momentum), or
drive the evolution of the extra coordinates of the barostat and
thermostat (
is a coupling
term between the center of mass momenta and the barostat momentum), or
drive the evolution of the extra coordinates of the barostat and
thermostat (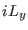 and
and 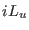 ). The time scale dynamics of these
terms depends not only on the potential subdivision and on the
parameters
). The time scale dynamics of these
terms depends not only on the potential subdivision and on the
parameters 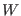 and
and 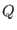 , but also on the type of
scaling [27]. When the molecular scaling is adopted the
dynamics of the virial term
, but also on the type of
scaling [27]. When the molecular scaling is adopted the
dynamics of the virial term
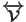 contains contributions only from the
intermolecular potential since the barostat is coupled only to the
center of mass coordinates (see Eq. (3.29)).
Indeed, the net force acting on the molecular center of mass
is independent on the intramolecular potential, since the latter
is invariant under rigid translation of the molecules. When atomic
scaling or group (i.e. sub-molecular) scaling is adopted, the virial
contains contributions only from the
intermolecular potential since the barostat is coupled only to the
center of mass coordinates (see Eq. (3.29)).
Indeed, the net force acting on the molecular center of mass
is independent on the intramolecular potential, since the latter
is invariant under rigid translation of the molecules. When atomic
scaling or group (i.e. sub-molecular) scaling is adopted, the virial
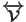 (see Eq. (3.39)) depends also on the fast
intramolecular such as stretching motions. In this case the time scale of the
barostat coordinate is no longer
slow, unless the parameter W is changed. For standard values of W,
selected to obtain an efficient
sampling of the
(see Eq. (3.39)) depends also on the fast
intramolecular such as stretching motions. In this case the time scale of the
barostat coordinate is no longer
slow, unless the parameter W is changed. For standard values of W,
selected to obtain an efficient
sampling of the 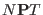 phase space [99,80], the barostat
dependent Liouvilleans, Eqs. (3.60,3.59), have time scale
dynamics comparable to that of the intramolecular Liouvillean
phase space [99,80], the barostat
dependent Liouvilleans, Eqs. (3.60,3.59), have time scale
dynamics comparable to that of the intramolecular Liouvillean 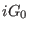 and therefore must be associated with this
term3.9.
and therefore must be associated with this
term3.9.
Thus, the molecular split of the Liouvillean is hence given by
whereas the atomic split is
For both scaling, a simple Hermitian factorization of the total time propagator
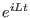 yields the double time discrete propagator
yields the double time discrete propagator
where
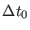 , the small time step, must be selected according
to the intramolecular time scale whereas
, the small time step, must be selected according
to the intramolecular time scale whereas
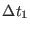 , the large
time step, must be selected according to the time scale of the
intermolecular motions. We already know that the propagator
(3.71) cannot generate a symplectic. The alert reader
may also have noticed that in this case the symmetric form of the
multiple time step propagator Eq. (3.71) does not imply
necessarily time reversibility. Some operators appearing in the
definition of
, the large
time step, must be selected according to the time scale of the
intermolecular motions. We already know that the propagator
(3.71) cannot generate a symplectic. The alert reader
may also have noticed that in this case the symmetric form of the
multiple time step propagator Eq. (3.71) does not imply
necessarily time reversibility. Some operators appearing in the
definition of 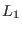 (e.g.
(e.g. 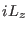 and
and 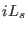 ) for the molecular
scaling and in the definitions of
) for the molecular
scaling and in the definitions of 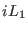 and
and 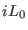 for the atomic
scaling are in fact non commuting. We have seen in section
2.2 that first order approximation of non commuting
propagators yields time irreversible algorithms. We can render the
propagator in Eq. (3.71) time reversible by using second
order symmetric approximant (i.e. Trotter approximation) for any two
non commuting operators. For example in the case of the molecular
scaling, when we propagate in Eq. (3.71) the slow propagator
for the atomic
scaling are in fact non commuting. We have seen in section
2.2 that first order approximation of non commuting
propagators yields time irreversible algorithms. We can render the
propagator in Eq. (3.71) time reversible by using second
order symmetric approximant (i.e. Trotter approximation) for any two
non commuting operators. For example in the case of the molecular
scaling, when we propagate in Eq. (3.71) the slow propagator
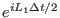 for half time step, we may use the following
second order
for half time step, we may use the following
second order
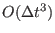 split
split
An alternative simpler and equally accurate approach when dealing with
non commuting operators is simply to preserve the unitarity by
reversing the order of the operators in the first order factorization
of the right and left operators of Eq. (3.71) without
resorting to locally second order
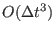 approximation like
in Eq. (3.72). Again for the molecular scaling, this is easily
done by using the approximant
approximation like
in Eq. (3.72). Again for the molecular scaling, this is easily
done by using the approximant
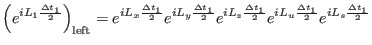 |
|
|
(3.72) |
for the left propagator, and
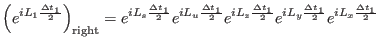 |
|
|
(3.73) |
for the rightmost propagator. Note that
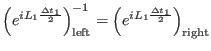 |
|
|
(3.74) |
Inserting these approximations into (3.71)
the overall integrator is found to be time
reversible and second order. Time reversible integrators are in fact
always even order and hence at least second
order [71,68].
Therefore the overall molecular and atomic (or group)
discrete time propagators are given by
The propagator
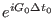 , defined in
Eq. (3.62), is further split according to the usual velocity
Verlet breakup of Eq. (2.22). Note that in case of
molecular scaling the ``slow'' coordinates
, defined in
Eq. (3.62), is further split according to the usual velocity
Verlet breakup of Eq. (2.22). Note that in case of
molecular scaling the ``slow'' coordinates
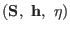 move with constant velocity during the
move with constant velocity during the  small times steps
since there is no ``fast'' force acting on them in the inner
integration. The explicit integration algorithm may be easily derived
for the two
propagators in Eqs. (3.76) and (3.77) using
the rule in Eq. (2.23) and its generalization:
small times steps
since there is no ``fast'' force acting on them in the inner
integration. The explicit integration algorithm may be easily derived
for the two
propagators in Eqs. (3.76) and (3.77) using
the rule in Eq. (2.23) and its generalization:
Where 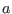 and
and
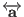 are a scalar and a matrix,
respectively. The exponential matrix
are a scalar and a matrix,
respectively. The exponential matrix
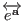 on the right hand side of Eq.
(3.78) is obtained by diagonalization of
on the right hand side of Eq.
(3.78) is obtained by diagonalization of
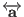 .
.
As stated before the dynamics generated by Eqs.
(3.23-3.27) or
(3.35-3.38) in the
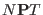 ensemble is
not Hamiltonian and hence we cannot speak of symplectic
integrators [100] for the
ensemble is
not Hamiltonian and hence we cannot speak of symplectic
integrators [100] for the 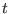 -flow's defined by
Eqs. (3.76,
3.77). The symplectic condition Eq. (2.8)
is violated at the level of the transformation (3.14-3.22)
which is not canonical. However, the algorithms generated
by Eqs. (3.76,3.77) are time reversible and
second order like the velocity Verlet. Several recent studies have
shown
[26,25,27] that these integrators for
the non microcanonical ensembles are also stable for long time
trajectories, as in case of the symplectic integrators for the NVE
ensemble.
-flow's defined by
Eqs. (3.76,
3.77). The symplectic condition Eq. (2.8)
is violated at the level of the transformation (3.14-3.22)
which is not canonical. However, the algorithms generated
by Eqs. (3.76,3.77) are time reversible and
second order like the velocity Verlet. Several recent studies have
shown
[26,25,27] that these integrators for
the non microcanonical ensembles are also stable for long time
trajectories, as in case of the symplectic integrators for the NVE
ensemble.
procacci
2021-12-29
![]() Liouvillean
Liouvillean
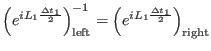
![]() ensemble is
not Hamiltonian and hence we cannot speak of symplectic
integrators [100] for the
ensemble is
not Hamiltonian and hence we cannot speak of symplectic
integrators [100] for the ![]() -flow's defined by
Eqs. (3.76,
3.77). The symplectic condition Eq. (2.8)
is violated at the level of the transformation (3.14-3.22)
which is not canonical. However, the algorithms generated
by Eqs. (3.76,3.77) are time reversible and
second order like the velocity Verlet. Several recent studies have
shown
[26,25,27] that these integrators for
the non microcanonical ensembles are also stable for long time
trajectories, as in case of the symplectic integrators for the NVE
ensemble.
-flow's defined by
Eqs. (3.76,
3.77). The symplectic condition Eq. (2.8)
is violated at the level of the transformation (3.14-3.22)
which is not canonical. However, the algorithms generated
by Eqs. (3.76,3.77) are time reversible and
second order like the velocity Verlet. Several recent studies have
shown
[26,25,27] that these integrators for
the non microcanonical ensembles are also stable for long time
trajectories, as in case of the symplectic integrators for the NVE
ensemble.