The Parrinello-Rahman-Nosé Hamiltonian and the
Equations of Motion
In order to derive the multiple time step integration algorithm using
the Liouville formalism described in the preceding sections we must
switch to the Hamiltonian formalism. Thus, we evaluate
the conjugate momenta of the coordinates
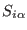 ,
,
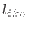 ,
,
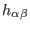 and
and 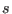 by taking the derivatives of the Lagrangian in
Eq. (3.6) with respect to corresponding velocities, i.e.
by taking the derivatives of the Lagrangian in
Eq. (3.6) with respect to corresponding velocities, i.e.
Where we have defined the symmetric matrix
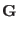 |
|
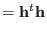 |
(3.11) |
The Hamiltonian of the system is obtained using the usual
Legendre transformation [72]
One obtains
In the extended systems formulation we always deal with real and virtual variables. The virtual variables in the Hamiltonian
(3.13) are the scaled coordinates and momenta
while the unscaled variables (e.g
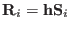 or
or
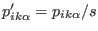 are the real counterpart. The variable
are the real counterpart. The variable 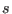 in
the Nosé formulation plays the role of a time scaling
[86,80,94]. The above Hamiltonian is given in
terms of virtual variables and in term of a virtual time and is
indeed a true Hamiltonian function and has corresponding
equation of motions that can be obtained applying
Eq. (2.3) with
in
the Nosé formulation plays the role of a time scaling
[86,80,94]. The above Hamiltonian is given in
terms of virtual variables and in term of a virtual time and is
indeed a true Hamiltonian function and has corresponding
equation of motions that can be obtained applying
Eq. (2.3) with
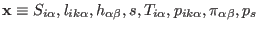 in a standard fashion.
Nonetheless, the equations of motions in
terms of these virtual variable are inadequate for several reasons
since for example one would deal with a fluctuating time
step [86,94]. It is therefore convenient to work in
terms of real momenta and real time. The real momenta are related to the
virtual counterpart through the relations
in a standard fashion.
Nonetheless, the equations of motions in
terms of these virtual variable are inadequate for several reasons
since for example one would deal with a fluctuating time
step [86,94]. It is therefore convenient to work in
terms of real momenta and real time. The real momenta are related to the
virtual counterpart through the relations
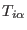 |
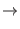 |
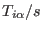 |
(3.14) |
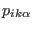 |
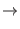 |
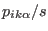 |
(3.15) |
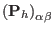 |
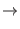 |
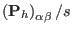 |
(3.16) |
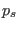 |
 |
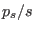 |
(3.17) |
It is also convenient [26] to introduce new center of mass
momenta as
such that the corresponding velocities may be obtained directly
without the knowledge of
the ``coordinates'' 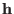 in
in 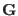 3.4, namely
3.4, namely
Finally, a real time formulation and a new dynamical variable
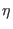 are adopted:
are adopted:
The equations of motions for the newly adopted set of dynamical
variables are easily obtained from the true Hamiltonian in Eq.
(3.13) and then using Eqs. (3.14-3.22)
to rewrite the resulting equations in terms of the new momenta. In so
doing, we obtain:
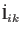 |
 |
 |
(3.22) |
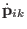 |
 |
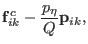 |
(3.23) |
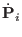 |
 |
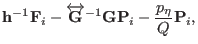 |
(3.24) |
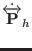 |
 |
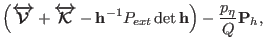 |
(3.25) |
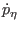 |
 |
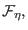 |
(3.26) |
It can be verified that the conserved quantity
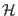 is associated with the above equations of motion, namely
is associated with the above equations of motion, namely
The atomic force
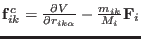 includes a constraint force contribution which guarantees that the
center of mass in the intramolecular frame of the
includes a constraint force contribution which guarantees that the
center of mass in the intramolecular frame of the
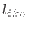 coordinates
remains at the origin.
coordinates
remains at the origin.
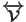 and
and
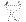 are the virial
and ideal gas contribution to the internal pressure tensor
are the virial
and ideal gas contribution to the internal pressure tensor
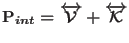 and they are defined as3.5
and they are defined as3.5
Finally
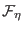 is the force driving the Nosé thermostat
is the force driving the Nosé thermostat
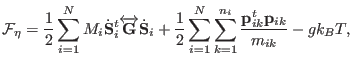 |
(3.29) |
with 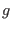 equal to the number of all degrees of freedom
equal to the number of all degrees of freedom 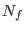 including those of the barostat3.6.
including those of the barostat3.6.
Eqs. (3.14-3.21) define a generalized coordinates
transformation of the kind of Eq. (2.4). This
transformation is non canonical, i.e. the Jacobian matrix of the
transformation from the virtual coordinates does not obey
Eq. (2.8). This means that 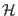 in terms of the new
coordinates Eq. (3.28) is ``only'' a constant of motion,
but is no longer a true Hamiltonian: application of
Eq. (2.1) does not lead to
Eqs. (3.23-3.27). Simulations using the real
variables are not Hamiltonian in nature in the sense that the phase
space of the real variables is compressible [96] and that
Liouville theorem is not satisfied [91]. This
``strangeness'' in the dynamics of the real variables in the extended
systems does not of course imply that the sampling of the
configurational real space is incorrect. To show this, it
suffices to evaluate the partition function for a microcanonical
distribution of the kind
in terms of the new
coordinates Eq. (3.28) is ``only'' a constant of motion,
but is no longer a true Hamiltonian: application of
Eq. (2.1) does not lead to
Eqs. (3.23-3.27). Simulations using the real
variables are not Hamiltonian in nature in the sense that the phase
space of the real variables is compressible [96] and that
Liouville theorem is not satisfied [91]. This
``strangeness'' in the dynamics of the real variables in the extended
systems does not of course imply that the sampling of the
configurational real space is incorrect. To show this, it
suffices to evaluate the partition function for a microcanonical
distribution of the kind
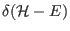 , with
, with 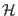 being given by Eq. (3.28). The Jacobian of the
transformation of Eqs. (3.14-3.22) must be included
in the integration with respect to the real coordinates when
evaluating the partition function for the extended system. If the
equations of motion in terms of the transformed coordinates are known,
this Jacobian,
being given by Eq. (3.28). The Jacobian of the
transformation of Eqs. (3.14-3.22) must be included
in the integration with respect to the real coordinates when
evaluating the partition function for the extended system. If the
equations of motion in terms of the transformed coordinates are known,
this Jacobian,
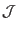 , can be readily computed from the
relation [73]:
, can be readily computed from the
relation [73]:
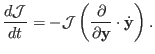 |
(3.30) |
Where 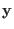 has the usual meaning of phase space vector
containing all independent coordinates and momenta of the
systems. Inserting the equations of motion of Eq. (3.27) into
Eq. (3.31) and integrating by separation of variables yields
has the usual meaning of phase space vector
containing all independent coordinates and momenta of the
systems. Inserting the equations of motion of Eq. (3.27) into
Eq. (3.31) and integrating by separation of variables yields
![$\displaystyle {\cal J} = e^{ N_{f} \eta } \left [ \det {\bf h}\right ]^{6 N}.$](img330.png) |
(3.31) |
Using (3.32) and integrating out the thermostat degrees
of freedom, the partition function can be
easily shown [91,97] to be equivalent to that
that of 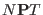 ensemble, i.e.
ensemble, i.e.
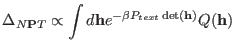 |
|
|
(3.32) |
with
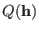 being the canonical distribution of a system with
cell of shape and size define by the columns of
being the canonical distribution of a system with
cell of shape and size define by the columns of 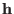 .3.7
.3.7
procacci
2021-12-29
![]() is associated with the above equations of motion, namely
is associated with the above equations of motion, namely
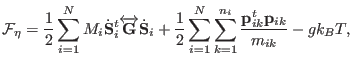
![]() in terms of the new
coordinates Eq. (3.28) is ``only'' a constant of motion,
but is no longer a true Hamiltonian: application of
Eq. (2.1) does not lead to
Eqs. (3.23-3.27). Simulations using the real
variables are not Hamiltonian in nature in the sense that the phase
space of the real variables is compressible [96] and that
Liouville theorem is not satisfied [91]. This
``strangeness'' in the dynamics of the real variables in the extended
systems does not of course imply that the sampling of the
configurational real space is incorrect. To show this, it
suffices to evaluate the partition function for a microcanonical
distribution of the kind
in terms of the new
coordinates Eq. (3.28) is ``only'' a constant of motion,
but is no longer a true Hamiltonian: application of
Eq. (2.1) does not lead to
Eqs. (3.23-3.27). Simulations using the real
variables are not Hamiltonian in nature in the sense that the phase
space of the real variables is compressible [96] and that
Liouville theorem is not satisfied [91]. This
``strangeness'' in the dynamics of the real variables in the extended
systems does not of course imply that the sampling of the
configurational real space is incorrect. To show this, it
suffices to evaluate the partition function for a microcanonical
distribution of the kind
![]() , with
, with ![]() being given by Eq. (3.28). The Jacobian of the
transformation of Eqs. (3.14-3.22) must be included
in the integration with respect to the real coordinates when
evaluating the partition function for the extended system. If the
equations of motion in terms of the transformed coordinates are known,
this Jacobian,
being given by Eq. (3.28). The Jacobian of the
transformation of Eqs. (3.14-3.22) must be included
in the integration with respect to the real coordinates when
evaluating the partition function for the extended system. If the
equations of motion in terms of the transformed coordinates are known,
this Jacobian,
![]() , can be readily computed from the
relation [73]:
, can be readily computed from the
relation [73]: