The starting point of our derivation of the multilevel integrator
for the NPT ensemble is the Parrinello-Rahman-Nosé Lagrangian for
a molecular system with 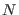 molecules or groups 3.2 each containing
molecules or groups 3.2 each containing 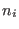 atoms
and subject to a potential
atoms
and subject to a potential 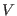 .
In order to construct the Lagrangian we
define a coordinate scaling and a velocity scaling, i.e.
.
In order to construct the Lagrangian we
define a coordinate scaling and a velocity scaling, i.e.
Here, the indices 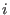 and
and 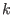 refer to molecules and atoms,
respectively, while Greek letters are used to label the Cartesian
components.
refer to molecules and atoms,
respectively, while Greek letters are used to label the Cartesian
components.
 is the
is the 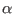 component of the coordinates of
the
component of the coordinates of
the 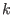 -th atom belonging to the
-th atom belonging to the 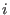 -th molecule;
-th molecule;
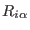 is the center
of mass coordinates;
is the center
of mass coordinates;
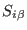 is the scaled coordinate of the
is the scaled coordinate of the
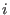 -th molecular center of mass.
-th molecular center of mass.
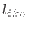 is the coordinate of
the
is the coordinate of
the 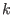 -th atom belonging to the
-th atom belonging to the 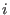 -th molecule expressed in a frame
parallel at any instant to the fixed laboratory frame, but with origin
on the instantaneous molecular center of mass. The set of
-th molecule expressed in a frame
parallel at any instant to the fixed laboratory frame, but with origin
on the instantaneous molecular center of mass. The set of
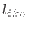 coordinates satisfies
coordinates satisfies 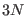 constraints of the type
constraints of the type
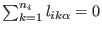 .
.
The matrix 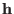 and the variable
and the variable 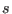 control the pressure an
temperature of the extended system, respectively.
The columns of the matrix
control the pressure an
temperature of the extended system, respectively.
The columns of the matrix 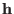 are the
Cartesian components of the cell edges with respect to a fixed frame.
The elements of this matrix allow the simulation cell to change
shape and size and are sometimes called the ``barostat''
coordinates. The volume of the MD cell is related to
are the
Cartesian components of the cell edges with respect to a fixed frame.
The elements of this matrix allow the simulation cell to change
shape and size and are sometimes called the ``barostat''
coordinates. The volume of the MD cell is related to 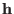 through the relation
through the relation
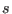 is the coordinates of the so-called ``Nosé thermostat''
and is coupled to the intramolecular and center of mass velocities,
is the coordinates of the so-called ``Nosé thermostat''
and is coupled to the intramolecular and center of mass velocities,
We define the ``potentials'' depending on the thermodynamic
variables 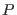 and
and 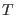
Where 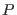 is
the external pressure of the system,
is
the external pressure of the system,
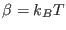 , and
, and 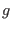 is a
constant related to total the number of degrees of freedom in the
system. This constant is chosen to correctly sample the
is a
constant related to total the number of degrees of freedom in the
system. This constant is chosen to correctly sample the 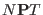 distribution function.
distribution function.
The extended 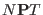 Lagrangian is then defined as
Lagrangian is then defined as
The arbitrary parameters 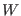 and
and 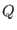 are the ``masses'' of the barostat
and of the thermostats, respectively3.3. They
do not affect the sampled distribution function but only the sampling
efficiency [26,94,95].
For a detailed discussion of the sampling properties of this
Lagrangian the reader is referred to Refs. [91,27].
are the ``masses'' of the barostat
and of the thermostats, respectively3.3. They
do not affect the sampled distribution function but only the sampling
efficiency [26,94,95].
For a detailed discussion of the sampling properties of this
Lagrangian the reader is referred to Refs. [91,27].
procacci
2021-12-29
![]() and the variable
and the variable ![]() control the pressure an
temperature of the extended system, respectively.
The columns of the matrix
control the pressure an
temperature of the extended system, respectively.
The columns of the matrix ![]() are the
Cartesian components of the cell edges with respect to a fixed frame.
The elements of this matrix allow the simulation cell to change
shape and size and are sometimes called the ``barostat''
coordinates. The volume of the MD cell is related to
are the
Cartesian components of the cell edges with respect to a fixed frame.
The elements of this matrix allow the simulation cell to change
shape and size and are sometimes called the ``barostat''
coordinates. The volume of the MD cell is related to ![]() through the relation
through the relation
![]() and
and ![]()
![]() Lagrangian is then defined as
Lagrangian is then defined as