Subdivision the Non Bonded Potential
In addition to the long range electrostatic contributions,
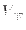 and
and
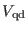 , given in Eqs. (4.20,4.21), more short
range forces play a significant role in the total non bonded
potential energy. The latter can be written as:
, given in Eqs. (4.20,4.21), more short
range forces play a significant role in the total non bonded
potential energy. The latter can be written as:
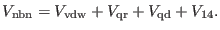 |
|
|
(4.36) |
Where,
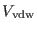 is the Lennard-Jones potential, namely
is the Lennard-Jones potential, namely
![$\displaystyle V_{\rm vdw} = {\sum_{i < j}^N}^{\prime} 4 \epsilon_{ij} \left [ \...
...j} } \right)^{12} - \left ( { \sigma_{ij} \over r_{ij} } \right )^{6} \right ].$](img604.png) |
(4.37) |
Here, the prime on the sum indicates that interactions between atoms
separated by less than three consecutive bonds must be omitted. The
term
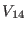 is typical for force fields of complex molecular
systems [3,5]. While non bonded forces between atoms
involved in the same covalent bond or angle bending interaction are
generally excluded, the potential between atoms separated by three
covalent bonds is retained and readjusted in various ways. In all
cases, the
is typical for force fields of complex molecular
systems [3,5]. While non bonded forces between atoms
involved in the same covalent bond or angle bending interaction are
generally excluded, the potential between atoms separated by three
covalent bonds is retained and readjusted in various ways. In all
cases, the
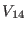 term remains in general a very stiff and, hence, a
fast varying term. The computational cost of the
term remains in general a very stiff and, hence, a
fast varying term. The computational cost of the
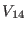 contribution is very small compared to other non bonded interactions.
Thus, it is safer to assigns this potential term to the slowest
intramolecular reference system potential
contribution is very small compared to other non bonded interactions.
Thus, it is safer to assigns this potential term to the slowest
intramolecular reference system potential
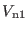 of Eq.
(4.19).
of Eq.
(4.19).
The
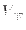 reciprocal lattice term, including the correction
due to the excluded or partially excluded (i.e. the electrostatic
part of
reciprocal lattice term, including the correction
due to the excluded or partially excluded (i.e. the electrostatic
part of
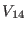 )
interactions cannot be split when using SPME and must be assigned
altogether to only one reference system. The time scale of the potential
)
interactions cannot be split when using SPME and must be assigned
altogether to only one reference system. The time scale of the potential
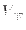 depends on the convergence parameter
depends on the convergence parameter 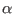 . Indeed, this constant
controls the relative weights of the reciprocal lattice energy
. Indeed, this constant
controls the relative weights of the reciprocal lattice energy
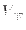 , and of the direct lattice energy
, and of the direct lattice energy
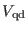 . By increasing
. By increasing
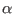 , one increases the weight of the reciprocal lattice
contribution
, one increases the weight of the reciprocal lattice
contribution
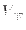 to the total Coulomb energy. When using SPME the
cost of the reciprocal lattice sums is cut down dramatically and,
therefore, the use of large
to the total Coulomb energy. When using SPME the
cost of the reciprocal lattice sums is cut down dramatically and,
therefore, the use of large 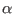 's becomes helpful to reduce the
computational burden of the direct lattice calculation. For a value of
's becomes helpful to reduce the
computational burden of the direct lattice calculation. For a value of
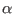 increased beyond a certain limit, there is no longer a computational
gain, since the pair distances must always be
evaluated in direct space until convergence of the Lennard-Jones
energy (usually occurring at a 10 Å cutoff).
Furthermore,
the larger is
increased beyond a certain limit, there is no longer a computational
gain, since the pair distances must always be
evaluated in direct space until convergence of the Lennard-Jones
energy (usually occurring at a 10 Å cutoff).
Furthermore,
the larger is 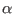 , the more short-ranged and fast varying becomes the
potential
, the more short-ranged and fast varying becomes the
potential
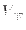 , thus requiring short time steps to integrate
correctly the equations of motion. A good compromise for
, thus requiring short time steps to integrate
correctly the equations of motion. A good compromise for
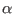 , valid for cell of any shape and size, is
, valid for cell of any shape and size, is 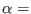 0.4-0.5.
0.4-0.5.
The direct space potential is separated [13,27]
in three contributions
according to the interaction distance. The overall non bonded potential
breakup is therefore
where the superscripts 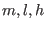 of the direct space term
of the direct space term
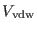 and
and
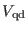 refer to the short, medium and long range non-bonded
interactions, respectively. The
refer to the short, medium and long range non-bonded
interactions, respectively. The  -th reference system includes
non-bonded direct space interactions at short range, typically
between 0 to
-th reference system includes
non-bonded direct space interactions at short range, typically
between 0 to 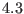 -
-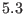 Å.
Å. 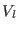 contains both the medium
range direct space potential, with a typical range of
contains both the medium
range direct space potential, with a typical range of 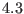 -
-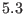 to
to
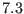 -
-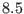 Å, and the reciprocal space term,
Å, and the reciprocal space term,
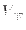 . Finally, the
. Finally, the
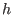 -th reference system, which is the most slowly varying contains, the
remaining direct space interactions from
-th reference system, which is the most slowly varying contains, the
remaining direct space interactions from 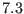 -
-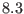 Å to cutoff
distance. As the simulations proceeds the particles seen by a target
particle may cross from one region to an other, while the number of two
body contacts in one distance class [19] or reference
system potential must be continuously updated. Instabilities caused by
this flow across potential shell boundaries are generally handled by
multiplying
the pair potential by a group-based switching
function [24]4.3.
Thus, at any distance
Å to cutoff
distance. As the simulations proceeds the particles seen by a target
particle may cross from one region to an other, while the number of two
body contacts in one distance class [19] or reference
system potential must be continuously updated. Instabilities caused by
this flow across potential shell boundaries are generally handled by
multiplying
the pair potential by a group-based switching
function [24]4.3.
Thus, at any distance 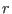 the direct space
potential
the direct space
potential 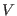 can be written schematically as:
can be written schematically as:
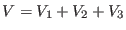 |
(4.39) |
with
where 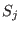 is the switching function for the three shells,
is the switching function for the three shells, 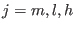 defined as:
defined as:
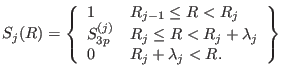 |
(4.43) |
Table:
| Component |
Contributions |
Spherical Shells |
Time step |
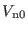 |
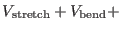 |
- |
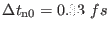 |
| |
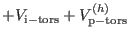 |
|
|
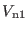 |
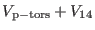 |
- |
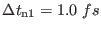 |
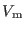 |
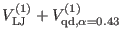 |
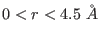 |
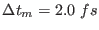 |
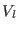 |
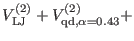 |
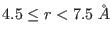 |
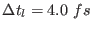 |
| |
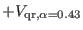 |
|
|
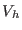 |
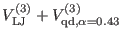 |
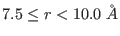 |
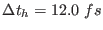 |
Here, 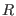 is the intergroup distance and
is the intergroup distance and 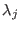 is the healing
interval for the
is the healing
interval for the 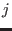 -th shell. While
-th shell. While 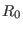 is zero,
is zero,
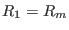 ,
,
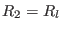 , and
, and
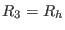 are the short, medium, long range
shell radius, respectively. The switching
are the short, medium, long range
shell radius, respectively. The switching
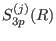 is 1 at
is 1 at
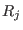 and goes monotonically to 0 at
and goes monotonically to 0 at
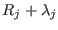 . Provided
that
. Provided
that
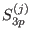 and its derivatives are continuous at
and its derivatives are continuous at 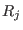 and
and
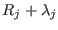 , the analytical form of
, the analytical form of 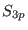 in the healing
interval is arbitrary [16,20,24,13].
The full breakup for an AMBER type force field along with the
integration time steps, valid for any complex molecular system with strong
electrostatic interactions, is summarize in table II. The
corresponding five time steps integration algorithm for the NVE
ensemble is given by
in the healing
interval is arbitrary [16,20,24,13].
The full breakup for an AMBER type force field along with the
integration time steps, valid for any complex molecular system with strong
electrostatic interactions, is summarize in table II. The
corresponding five time steps integration algorithm for the NVE
ensemble is given by
where
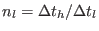 ,
,
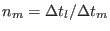 ,
,
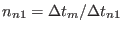 ,
,
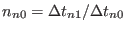 .
The explicit integration algorithm can be easily derived applying
the five-fold discrete time propagator (4.46) to
the state vector
.
The explicit integration algorithm can be easily derived applying
the five-fold discrete time propagator (4.46) to
the state vector
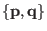 at time 0 using the rule
Eq. (2.23). The efficiency and accuracy for energy
conservation of this r-RESPA symplectic and reversible integrator
have been discussed extensively in Refs. [13,2].
Extension of this subdivision to non NVE simulation is described
in Ref. [27].
at time 0 using the rule
Eq. (2.23). The efficiency and accuracy for energy
conservation of this r-RESPA symplectic and reversible integrator
have been discussed extensively in Refs. [13,2].
Extension of this subdivision to non NVE simulation is described
in Ref. [27].
procacci
2021-12-29
![]() reciprocal lattice term, including the correction
due to the excluded or partially excluded (i.e. the electrostatic
part of
reciprocal lattice term, including the correction
due to the excluded or partially excluded (i.e. the electrostatic
part of
![]() )
interactions cannot be split when using SPME and must be assigned
altogether to only one reference system. The time scale of the potential
)
interactions cannot be split when using SPME and must be assigned
altogether to only one reference system. The time scale of the potential
![]() depends on the convergence parameter
depends on the convergence parameter ![]() . Indeed, this constant
controls the relative weights of the reciprocal lattice energy
. Indeed, this constant
controls the relative weights of the reciprocal lattice energy
![]() , and of the direct lattice energy
, and of the direct lattice energy
![]() . By increasing
. By increasing
![]() , one increases the weight of the reciprocal lattice
contribution
, one increases the weight of the reciprocal lattice
contribution
![]() to the total Coulomb energy. When using SPME the
cost of the reciprocal lattice sums is cut down dramatically and,
therefore, the use of large
to the total Coulomb energy. When using SPME the
cost of the reciprocal lattice sums is cut down dramatically and,
therefore, the use of large ![]() 's becomes helpful to reduce the
computational burden of the direct lattice calculation. For a value of
's becomes helpful to reduce the
computational burden of the direct lattice calculation. For a value of
![]() increased beyond a certain limit, there is no longer a computational
gain, since the pair distances must always be
evaluated in direct space until convergence of the Lennard-Jones
energy (usually occurring at a 10 Å cutoff).
Furthermore,
the larger is
increased beyond a certain limit, there is no longer a computational
gain, since the pair distances must always be
evaluated in direct space until convergence of the Lennard-Jones
energy (usually occurring at a 10 Å cutoff).
Furthermore,
the larger is ![]() , the more short-ranged and fast varying becomes the
potential
, the more short-ranged and fast varying becomes the
potential
![]() , thus requiring short time steps to integrate
correctly the equations of motion. A good compromise for
, thus requiring short time steps to integrate
correctly the equations of motion. A good compromise for
![]() , valid for cell of any shape and size, is
, valid for cell of any shape and size, is ![]() 0.4-0.5.
0.4-0.5.