Before we discuss the non bonded multiple time step separation it is
useful to describe in some details one of the most advanced techniques
to handle long range forces. Indeed, this type of non bonded forces are the
most cumbersome to handle and deserve closer scrutiny.
In the recent literature, a variety of techniques are available to handle the
problem of long range interactions in computer simulations of charged
particles at different level of approximation [30,31,12].
In this section, we shall focus on the Ewald summation method for
the treatment of long range interactions in periodic
systems [32,33,101]. The Ewald method gives the
exact result for the electrostatic energy of a periodic
system consisting of an infinitely replicated neutral box of charged
particles.
The method is the natural choice in MD simulations
of complex molecular system with PBC.
The Ewald potential [33] is given by
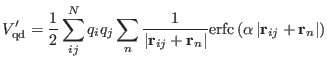 |
(4.20) |
![$\displaystyle V_{\rm qr} = \left [ {1 \over 2 \pi V} \sum_{{\bf m} \ne 0}^{\inf...
... {\bf m} \right ) - {\alpha \over \pi^{1/2}} \sum_i q_i^2 \right ] - V_{intra}.$](img522.png) |
(4.21) |
with
where,
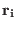 is the vector position of the atomic charge
is the vector position of the atomic charge
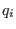 ,
,
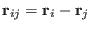 ,
,
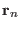 is
a vector of the direct lattice,
is
a vector of the direct lattice,
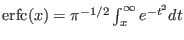 is the complementary error function,
is the complementary error function,
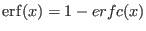 ,
, 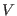 the unit cell volume,
the unit cell volume, 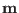 a reciprocal lattice
vector and
a reciprocal lattice
vector and 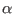 is the Ewald convergence parameter. In the direct
lattice part, Eq. (4.20), the prime indicates that
intramolecular excluded contacts4.1are omitted. In addition, in Eq.
(4.21) the term
is the Ewald convergence parameter. In the direct
lattice part, Eq. (4.20), the prime indicates that
intramolecular excluded contacts4.1are omitted. In addition, in Eq.
(4.21) the term
 subtracts, in direct space, the
intra-molecular energy between bonded pairs, which is automatically
included in the right hand side of that equation. Consequently, the
summation on
subtracts, in direct space, the
intra-molecular energy between bonded pairs, which is automatically
included in the right hand side of that equation. Consequently, the
summation on 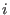 and
and 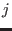 in Eq. (4.23) goes over all the
excluded intra-molecular contacts. We must point out that in the
Ewald potential given above, we have implicitly assumed the so-called
``tin-foil'' boundary conditions: the Ewald sphere is immersed in a
perfectly conducting medium and hence the dipole term on the surface
of the Ewald sphere is zero [33].
For increasingly large systems the computational cost of standard
Ewald summation, which scales with
in Eq. (4.23) goes over all the
excluded intra-molecular contacts. We must point out that in the
Ewald potential given above, we have implicitly assumed the so-called
``tin-foil'' boundary conditions: the Ewald sphere is immersed in a
perfectly conducting medium and hence the dipole term on the surface
of the Ewald sphere is zero [33].
For increasingly large systems the computational cost of standard
Ewald summation, which scales with 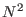 , becomes too large for
practical applications. Alternative algorithms which scale with a
smaller power of
, becomes too large for
practical applications. Alternative algorithms which scale with a
smaller power of 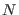 than standard Ewald have been proposed in the
past. Among the fastest algorithms designed for periodic systems is
the particle mesh Ewald algorithm (PME)[34,35],
inspired by the particle mesh method of Hockney and
Eastwood [36]. Here, a multidimensional piece-wise
interpolation approach is used to compute the reciprocal lattice
energy,
than standard Ewald have been proposed in the
past. Among the fastest algorithms designed for periodic systems is
the particle mesh Ewald algorithm (PME)[34,35],
inspired by the particle mesh method of Hockney and
Eastwood [36]. Here, a multidimensional piece-wise
interpolation approach is used to compute the reciprocal lattice
energy,
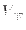 , of Eq. 4.21, while the direct part,
, of Eq. 4.21, while the direct part,
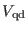 , is computed straightforwardly. The low computational
cost of the PME method allows the choice of large values of the Ewald
convergence parameter
, is computed straightforwardly. The low computational
cost of the PME method allows the choice of large values of the Ewald
convergence parameter 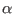 , as compared to those used in
conventional Ewald. Correspondingly, shorter cutoffs in the direct
space Ewald sum
, as compared to those used in
conventional Ewald. Correspondingly, shorter cutoffs in the direct
space Ewald sum
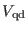 may be adopted. If
may be adopted. If
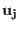 is the
scaled fractional coordinate of the
is the
scaled fractional coordinate of the 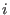 -th particle, the charge
weighted structure factor,
-th particle, the charge
weighted structure factor,
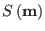 in
Eq. (4.22), can be rewritten as:
in
Eq. (4.22), can be rewritten as:
![$\displaystyle S \left ( {\bf m} \right ) = \sum_{j=1}^{N} q_{j} \exp \left [ 2 ...
...{1}} + {m_{2}u_{2j} \over K_{2}} + {m_{3}u_{3j} \over K_{3}} \right ) \right ].$](img541.png) |
(4.24) |
Where, 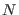 is the number of particles,
is the number of particles,
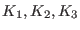 and
and
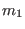 ,
, 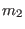 ,
, 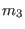 are integers. The
are integers. The
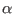 component of the scaled fractional coordinate for the
component of the scaled fractional coordinate for the 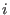 -th
atom can be written
as:4.2
-th
atom can be written
as:4.2
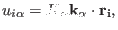 |
(4.25) |
where
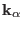 ,
,
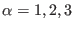 are the reciprocal lattice
basic vectors.
are the reciprocal lattice
basic vectors.
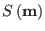 in Eq. (4.24) can be looked at
as a discrete Fourier transform (FT) of a set of charges placed irregularly
within the unit cell. Techniques have been devised in the past to
approximate
in Eq. (4.24) can be looked at
as a discrete Fourier transform (FT) of a set of charges placed irregularly
within the unit cell. Techniques have been devised in the past to
approximate
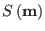 with expressions involving
Fourier transforms on a regular grid of points. Such approximations of
the weighted structure factor are computationally advantageous because
they can be evaluated by fast Fourier transforms (FFT). All these
FFT-based approaches involve, in some sense, a smearing of the
charges over nearby grid points to produce a regularly gridded charge
distribution. The PME method accomplishes this task by interpolation. Thus,
the complex exponential
with expressions involving
Fourier transforms on a regular grid of points. Such approximations of
the weighted structure factor are computationally advantageous because
they can be evaluated by fast Fourier transforms (FFT). All these
FFT-based approaches involve, in some sense, a smearing of the
charges over nearby grid points to produce a regularly gridded charge
distribution. The PME method accomplishes this task by interpolation. Thus,
the complex exponential
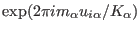 , computed at the position of the
, computed at the position of the
 -th charge in Eq. (4.24), are rewritten as a sum of
interpolation coefficients multiplied by their values at the nearby
grid points. In the smooth version of PME (SPME) [35],
which uses cardinal B-splines in place of the Lagrangian coefficients
adopted by PME, the sum is further multiplied by an
appropriate factor, namely:
-th charge in Eq. (4.24), are rewritten as a sum of
interpolation coefficients multiplied by their values at the nearby
grid points. In the smooth version of PME (SPME) [35],
which uses cardinal B-splines in place of the Lagrangian coefficients
adopted by PME, the sum is further multiplied by an
appropriate factor, namely:
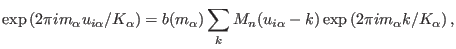 |
(4.26) |
where  is the order of the spline interpolation,
is the order of the spline interpolation,
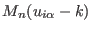 defines the coefficients of the cardinal
B-spline interpolation at the scaled coordinate
defines the coefficients of the cardinal
B-spline interpolation at the scaled coordinate
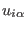 . In Eq.
(4.26) the sum over
. In Eq.
(4.26) the sum over 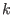 , representing the grid points, is
only over a finite range of integers, since the functions
, representing the grid points, is
only over a finite range of integers, since the functions 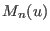 are zero outside the interval
are zero outside the interval
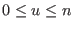 . It must be stressed
that the complex coefficients
. It must be stressed
that the complex coefficients 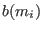 are independent of the charge
coordinates
are independent of the charge
coordinates 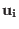 and need be computed only at the very
beginning of a simulation. A detailed derivation of the
and need be computed only at the very
beginning of a simulation. A detailed derivation of the
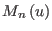 functions and of the
functions and of the
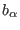 coefficients is
given in Ref. [35]. By inserting Eq. (4.26)
into Eq. (4.24),
coefficients is
given in Ref. [35]. By inserting Eq. (4.26)
into Eq. (4.24),
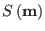 can be
rewritten as:
can be
rewritten as:
![$\displaystyle S({\bf m}) = b_{1}(m_{1}) b_{2}(m_{2}) b_{3}(m_{3}) {\cal F} \left [ Q \right ] \left ( m_{1},m_{2},m_{3} \right ),$](img560.png) |
(4.27) |
where
![$ {\cal F} \left [ Q \right ] \left ( m_{1},m_{2},m_{3} \right )$](img561.png) stands
for the discrete FT at the grid point
stands
for the discrete FT at the grid point
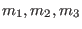 of the array
of the array
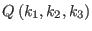 with
with
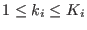 ,
,
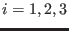 . The gridded
charge array,
. The gridded
charge array,
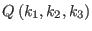 , is defined as:
, is defined as:
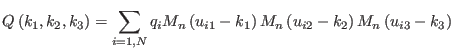 |
(4.28) |
Inserting the approximated structure factor of Eq. (4.27) into
Eq. (4.21) and using the fact that
![$ {\cal F}\left [ Q \right ]
\left ( -m_{1},
-m_{2}, -m_{3} \right ) = K_{1} K_{2} K_{3} {\cal F}^{-1} \left [ Q
\right ] \left ( m_{1} , m_{2},m_{3} \right )$](img567.png) , the SPME reciprocal
lattice energy can be then written as
, the SPME reciprocal
lattice energy can be then written as
with
Using the convolution theorem for FFT the energy (4.30)
can be rewritten as
We now use the identity
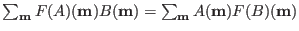 to arrive at
to arrive at
We first notice that
 does not depend on
the charge positions and that
does not depend on
the charge positions and that
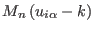 is differentiable for
is differentiable for 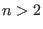 (which is always the case in practical
applications). Thus the force on each charge can be obtained by taking the
derivative of Eq. (4.35), namely
(which is always the case in practical
applications). Thus the force on each charge can be obtained by taking the
derivative of Eq. (4.35), namely
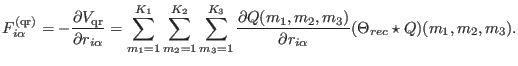 |
(4.35) |
In practice, the calculation is carried out according to the following
scheme: i) At each simulation step one computes the grid scaled
fractional coordinates
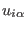 and fills an array with
and fills an array with 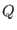 according to Eq. (4.28). At this stage, the derivative of the
according to Eq. (4.28). At this stage, the derivative of the
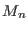 functions are also computed and stored in memory. ii) The
array containing
functions are also computed and stored in memory. ii) The
array containing 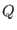 is then overwritten by
is then overwritten by
![$ {\cal F} \left [ Q \right
]$](img587.png) , i.e.
, i.e. 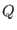 's 3-D Fourier transform. iii) Subsequently, the electrostatic energy
is computed via Eq. (4.30). At the same time, the array
containing
's 3-D Fourier transform. iii) Subsequently, the electrostatic energy
is computed via Eq. (4.30). At the same time, the array
containing
![$ {\cal F} \left [ Q \right
]$](img587.png) is overwritten by the product
of itself with the array containing
is overwritten by the product
of itself with the array containing 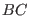 (computed at the very
beginning of the run). iv) The resulting array is then Fourier
transformed to obtain the convolution
(computed at the very
beginning of the run). iv) The resulting array is then Fourier
transformed to obtain the convolution
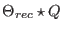 . v)
Finally, the forces are computed via Eq. (4.36) using the
previously stored derivatives of the
. v)
Finally, the forces are computed via Eq. (4.36) using the
previously stored derivatives of the 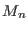 functions to recast
functions to recast
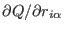 .
.
The memory requirements of the SPME method are limited.
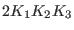 double precision real numbers are needed for the grid
charge array
double precision real numbers are needed for the grid
charge array 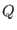 , while the calculation of the functions
, while the calculation of the functions
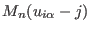 and their derivatives requires only
and their derivatives requires only
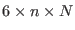 double precision real numbers. The
double precision real numbers. The
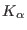 integers
determines the fineness of the grid along the
integers
determines the fineness of the grid along the 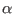 -th lattice vector of
the unit cell. The output accuracy of the energy and forces depends
on the SPME parameters: The
-th lattice vector of
the unit cell. The output accuracy of the energy and forces depends
on the SPME parameters: The 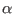 convergence parameter, the
grid spacing and the order
convergence parameter, the
grid spacing and the order  of the B-spline interpolation. For a
typical
of the B-spline interpolation. For a
typical
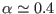 Å
Å 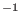 a relative accuracy between
a relative accuracy between
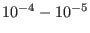 for the electrostatic energy are obtained when the
grid spacing is around 1 Å along each axis, and the order
for the electrostatic energy are obtained when the
grid spacing is around 1 Å along each axis, and the order  of the
of the
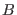 -spline interpolation is 4 or 5. A rigorous error analysis and a
comparison with standard Ewald summation can be found in Refs.
[35] and [102]. For further readings on the PME and
SPME techniques we refer to the original
papers [34,102,29,35].
-spline interpolation is 4 or 5. A rigorous error analysis and a
comparison with standard Ewald summation can be found in Refs.
[35] and [102]. For further readings on the PME and
SPME techniques we refer to the original
papers [34,102,29,35].
The power of the SPME algorithm, compared to the straightforward
implementation of the standard Ewald method, is indeed astonishing. In
Fig. (4.3) we report CPU timing obtained on a low end
43P/160MH IBM workstation for the evaluation of the reciprocal lattice
energy and forces via SPME for cyanobiphenil as a function of the
number of atoms in the system. Public domain 3-D FFT routines were used. The
algorithm is practically linear and for 12,000 particles SPME takes
only 2 CPU seconds to perform the calculation. A standard Ewald
simulation for a box
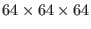 Å
Å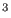 (i.e. with a
grid spacing in
(i.e. with a
grid spacing in 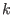 space of
space of
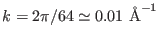 ) for
the same sample and at the same level of accuracy would have taken
several minutes.
) for
the same sample and at the same level of accuracy would have taken
several minutes.
procacci
2021-12-29
![]() in Eq. (4.24) can be looked at
as a discrete Fourier transform (FT) of a set of charges placed irregularly
within the unit cell. Techniques have been devised in the past to
approximate
in Eq. (4.24) can be looked at
as a discrete Fourier transform (FT) of a set of charges placed irregularly
within the unit cell. Techniques have been devised in the past to
approximate
![]() with expressions involving
Fourier transforms on a regular grid of points. Such approximations of
the weighted structure factor are computationally advantageous because
they can be evaluated by fast Fourier transforms (FFT). All these
FFT-based approaches involve, in some sense, a smearing of the
charges over nearby grid points to produce a regularly gridded charge
distribution. The PME method accomplishes this task by interpolation. Thus,
the complex exponential
with expressions involving
Fourier transforms on a regular grid of points. Such approximations of
the weighted structure factor are computationally advantageous because
they can be evaluated by fast Fourier transforms (FFT). All these
FFT-based approaches involve, in some sense, a smearing of the
charges over nearby grid points to produce a regularly gridded charge
distribution. The PME method accomplishes this task by interpolation. Thus,
the complex exponential
![]() , computed at the position of the
, computed at the position of the
![]() -th charge in Eq. (4.24), are rewritten as a sum of
interpolation coefficients multiplied by their values at the nearby
grid points. In the smooth version of PME (SPME) [35],
which uses cardinal B-splines in place of the Lagrangian coefficients
adopted by PME, the sum is further multiplied by an
appropriate factor, namely:
-th charge in Eq. (4.24), are rewritten as a sum of
interpolation coefficients multiplied by their values at the nearby
grid points. In the smooth version of PME (SPME) [35],
which uses cardinal B-splines in place of the Lagrangian coefficients
adopted by PME, the sum is further multiplied by an
appropriate factor, namely:
![]() and fills an array with
and fills an array with ![]() according to Eq. (4.28). At this stage, the derivative of the
according to Eq. (4.28). At this stage, the derivative of the
![]() functions are also computed and stored in memory. ii) The
array containing
functions are also computed and stored in memory. ii) The
array containing ![]() is then overwritten by
is then overwritten by
![]() , i.e.
, i.e. ![]() 's 3-D Fourier transform. iii) Subsequently, the electrostatic energy
is computed via Eq. (4.30). At the same time, the array
containing
's 3-D Fourier transform. iii) Subsequently, the electrostatic energy
is computed via Eq. (4.30). At the same time, the array
containing
![]() is overwritten by the product
of itself with the array containing
is overwritten by the product
of itself with the array containing ![]() (computed at the very
beginning of the run). iv) The resulting array is then Fourier
transformed to obtain the convolution
(computed at the very
beginning of the run). iv) The resulting array is then Fourier
transformed to obtain the convolution
![]() . v)
Finally, the forces are computed via Eq. (4.36) using the
previously stored derivatives of the
. v)
Finally, the forces are computed via Eq. (4.36) using the
previously stored derivatives of the ![]() functions to recast
functions to recast
![]() .
.
![]() double precision real numbers are needed for the grid
charge array
double precision real numbers are needed for the grid
charge array ![]() , while the calculation of the functions
, while the calculation of the functions
![]() and their derivatives requires only
and their derivatives requires only
![]() double precision real numbers. The
double precision real numbers. The
![]() integers
determines the fineness of the grid along the
integers
determines the fineness of the grid along the ![]() -th lattice vector of
the unit cell. The output accuracy of the energy and forces depends
on the SPME parameters: The
-th lattice vector of
the unit cell. The output accuracy of the energy and forces depends
on the SPME parameters: The ![]() convergence parameter, the
grid spacing and the order
convergence parameter, the
grid spacing and the order ![]() of the B-spline interpolation. For a
typical
of the B-spline interpolation. For a
typical
![]() Å
Å ![]() a relative accuracy between
a relative accuracy between
![]() for the electrostatic energy are obtained when the
grid spacing is around 1 Å along each axis, and the order
for the electrostatic energy are obtained when the
grid spacing is around 1 Å along each axis, and the order ![]() of the
of the
![]() -spline interpolation is 4 or 5. A rigorous error analysis and a
comparison with standard Ewald summation can be found in Refs.
[35] and [102]. For further readings on the PME and
SPME techniques we refer to the original
papers [34,102,29,35].
-spline interpolation is 4 or 5. A rigorous error analysis and a
comparison with standard Ewald summation can be found in Refs.
[35] and [102]. For further readings on the PME and
SPME techniques we refer to the original
papers [34,102,29,35].
![\includegraphics[height=8cm]{cpu.eps}](img598.png)