As we have seen in Sec. 2.3 the idea behind the
multiple time step scheme is that of the reference system which
propagates for a certain amount of time under the influence of some
unperturbed reference Hamiltonian, and then undergoes an
impulsive correction brought by the remainder of the
potential. The exact trajectory spanned by the complete Hamiltonian is
recovered by applying this impulsive correction onto the ``reference''
trajectory. We have also seen in the same section that, by subdividing
the interaction potential, we can determine as many ``nested''
reference systems as we wish.
The first step in defining a general protocol for the subdivision of the
bonded potential for complex molecular systems consists in identifying the
various time scales and their connection to the potential.
The interaction bonded potential in almost all popular force fields
is given as a function of the stretching, bending
and torsion internal coordinates and has the general form
where
Here, 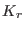 and
and
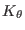 are the bonded force constants associated with
bond stretching and angles bending respectively, while
are the bonded force constants associated with
bond stretching and angles bending respectively, while 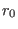 and
and
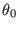 are their respective equilibrium values. In the torsional
potential,
are their respective equilibrium values. In the torsional
potential, 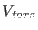 ,
, 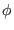 is the dihedral angle, while
is the dihedral angle, while
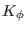 ,
,  and
and 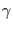 are constants.
are constants.
The characteristic time scale of a particular internal degrees of
freedom can be estimated assuming that this coordinate behaves like
a harmonic oscillator, uncoupled form the rest the other internal
degrees of freedom. Thus, the criterion for guiding the
subdivision of the potential in Eq. (4.2) is given by the
characteristic frequency of this uncoupled oscillator.
We now give, for each type of degree of freedom, practical formula to
evaluate the harmonic frequency from the force field constants
given in Eq. (4.3).
Stretching: The stretching frequencies are given by the well known expression
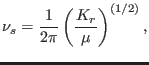 |
|
|
(4.4) |
where 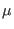 is reduced mass.
is reduced mass.
Bending: We shall assume for the sake of simplicity that the uncoupled bending
frequencies depends on the masses of the atom 1 and 3
(see Fig. 4.1), that is mass 2 is assumed to be infinity.
This turns out to be in general an excellent approximation for
bending involving hydrogen and a good approximation for
external bendings in large molecules involving masses of comparable
magnitude.
The frequency is obtained by writing the Lagrangian in polar
coordinates for the mechanical system depicted in Fig. 4.1. The
Cartesian coordinates are expressed in terms of the polar coordinates as
where the distance 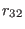 and
and 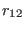 are constrained to the
equilibrium values. The velocities are then
are constrained to the
equilibrium values. The velocities are then
The Lagrangian for the uncoupled bending is then
The equation of motion
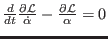 for the
for the 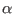 coordinate is given by
coordinate is given by
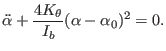 |
|
|
(4.11) |
Where,
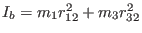 is the moment of
inertia about an axis passing by atom 3 and perpendicular to the
bending plane. Finally, the uncoupled bending frequency is given by
is the moment of
inertia about an axis passing by atom 3 and perpendicular to the
bending plane. Finally, the uncoupled bending frequency is given by
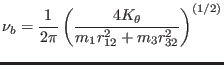 |
|
|
(4.12) |
Torsion: We limit our analysis to a purely torsional system (see
Fig. 4.1b ) where atoms 2 and 3 are held fixed, and all
bond distances
and the angle 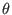 are constrained to their equilibrium values. The
system has only one degree of freedom, the dihedral angle
are constrained to their equilibrium values. The
system has only one degree of freedom, the dihedral angle 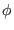 driven by the torsional potential
driven by the torsional potential 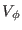 . Again we rewrite the
kinetic energy in terms of the bond distances, the dihedral angle and
the constant bend angle
. Again we rewrite the
kinetic energy in terms of the bond distances, the dihedral angle and
the constant bend angle 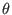 . For the kinetic energy, the only
relevant coordinates are now those of atoms 1 and 4:
. For the kinetic energy, the only
relevant coordinates are now those of atoms 1 and 4:
The Lagrangian in terms of the dihedral angle coordinate is then
where
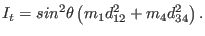 |
|
|
(4.15) |
Assuming small oscillations,
the potential may be approximated by a second order expansion around
the corresponding equilibrium dihedral angle 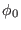
Substituting (4.16) into Eq . (4.14) and
then writing the Lagrange equation of motion for the coordinate 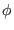 , one
obtains again a differential equation of a harmonic oscillator, namely
, one
obtains again a differential equation of a harmonic oscillator, namely
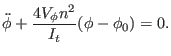 |
|
|
(4.17) |
Thus, the uncoupled torsional frequency is given by
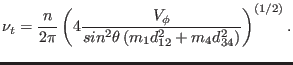 |
|
|
(4.18) |
For many all-atom force fields, improper torsions [3,6]
are modeled using a potential identical to that of the proper torsion
in Eq. (4.3) and hence in these cases
Eq. (4.18) applies also to the improper torsion uncoupled
frequency, provided that indices 1 and 4 refer to the lighter
atoms. In figure (4.2) we report the distribution of
frequencies for the hydrated protein Bovine Pancreatin Trypsin
Inhibitor (BPTI) using the AMBER [4] force field. The
distributions might be thought as a density of the uncoupled
intramolecular states of the system. As we can see in the figure
there is a relevant degree of overlap for the various internal degrees
of freedom. For example, ``slow'' degrees of freedom such as torsions
may be found up to 600 wavenumber, well inside the ``bending'' region;
these are usually improper or proper torsions involving hydrogen. It
is then inappropriate to assign such ``fast'' torsions involving
hydrogen to a slow reference system. We recall that in a multiple
time simulation the integration of a supposedly slow degree of freedom
with a excessively large time step is enough to undermine the entire
simulation.
In Fig. 4.2 we also notice that almost all the proper
torsions fall below 350 cm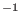 . An efficient and simple separation of
the intramolecular AMBER potential [27] assigns all bendings
stretching and the improper or proper torsions involving
hydrogen to a ``fast'' reference system labeled
. An efficient and simple separation of
the intramolecular AMBER potential [27] assigns all bendings
stretching and the improper or proper torsions involving
hydrogen to a ``fast'' reference system labeled 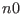 and all proper
torsions to a slower reference system labeled
and all proper
torsions to a slower reference system labeled 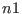 . The subdivision is
then
. The subdivision is
then
Where with
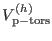 we indicate proper torsions involving
hydrogen. For the reference system
we indicate proper torsions involving
hydrogen. For the reference system
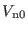 , the hydrogen stretching
frequencies are the fastest motions and the
, the hydrogen stretching
frequencies are the fastest motions and the
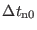 time step must be set to 0.2-0.3 fs. The
computational burden of this part of the potential is very limited,
since it involves mostly two or three body forces. For the reference
system
time step must be set to 0.2-0.3 fs. The
computational burden of this part of the potential is very limited,
since it involves mostly two or three body forces. For the reference
system
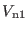 , the fastest motion is around 300 cm
, the fastest motion is around 300 cm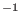 and the
time step
and the
time step
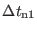 should be set to 1-1.5 fs. The
computational effort for the reference system potential
should be set to 1-1.5 fs. The
computational effort for the reference system potential 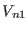 is
more important because of the numerous proper torsions of complex
molecular systems which
involve more expensive four body forces calculations. One may also notice that
some of the bendings which were assigned to the n0
reference system fall in the torsion frequency region and could be
therefore integrated with a time step much larger than
is
more important because of the numerous proper torsions of complex
molecular systems which
involve more expensive four body forces calculations. One may also notice that
some of the bendings which were assigned to the n0
reference system fall in the torsion frequency region and could be
therefore integrated with a time step much larger than
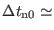 0.2-0.3. However, in a multiple time step integration,
this overlap is just inefficient, but certainly not dangerous. Indeed, no
instability may derive for integrating slow degrees of freedom with
exceedingly small time steps.
0.2-0.3. However, in a multiple time step integration,
this overlap is just inefficient, but certainly not dangerous. Indeed, no
instability may derive for integrating slow degrees of freedom with
exceedingly small time steps.
procacci
2021-12-29
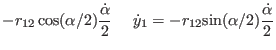
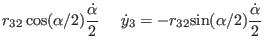
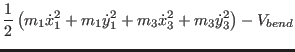
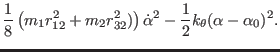
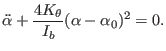
![]() are constrained to their equilibrium values. The
system has only one degree of freedom, the dihedral angle
are constrained to their equilibrium values. The
system has only one degree of freedom, the dihedral angle ![]() driven by the torsional potential
driven by the torsional potential ![]() . Again we rewrite the
kinetic energy in terms of the bond distances, the dihedral angle and
the constant bend angle
. Again we rewrite the
kinetic energy in terms of the bond distances, the dihedral angle and
the constant bend angle ![]() . For the kinetic energy, the only
relevant coordinates are now those of atoms 1 and 4:
. For the kinetic energy, the only
relevant coordinates are now those of atoms 1 and 4:
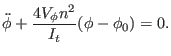
![\includegraphics[scale=0.6]{spct.eps}](img507.png)