Electrostatic Corrections for the Multiple Time Step
Simulation
In flexible molecular systems of large size, the
Ewald summation presents computational problems which are crucial to
constructing efficient and stable multiple time step
integrators [103,2]. We have seen that
intra-molecular Coulomb interactions between bonded atoms or between
atoms bonded to a common atom are excluded in most of the standard
force fields for protein simulation. In any practical implementation
of the Ewald method, the intra-molecular energy
 is
automatically included in the reciprocal space summation and is
subtracted in direct space (see Eqs. (4.23,4.21).
In actual simulations the reciprocal space sum is computed with a
finite accuracy whereas the intra-molecular term
is
automatically included in the reciprocal space summation and is
subtracted in direct space (see Eqs. (4.23,4.21).
In actual simulations the reciprocal space sum is computed with a
finite accuracy whereas the intra-molecular term
 , due
to the excluded Coulomb interactions, is computed exactly. This
clearly prevents the cancellation of the intra-molecular forces and
energies. When the stretching and bending
forces are integrated explicitly, the intra-molecular term due to the
excluded contacts varies rapidly with time and so does the
cancellation error. Consequently, instability may be observed when
integrating the reciprocal lattice forces in reference systems with
large time steps. The correction due to the truncation can be
evaluated by approximating the reciprocal lattice sum for the excluded
contacts in Eq. (4.21) to an integral in the 3-dimensional
, due
to the excluded Coulomb interactions, is computed exactly. This
clearly prevents the cancellation of the intra-molecular forces and
energies. When the stretching and bending
forces are integrated explicitly, the intra-molecular term due to the
excluded contacts varies rapidly with time and so does the
cancellation error. Consequently, instability may be observed when
integrating the reciprocal lattice forces in reference systems with
large time steps. The correction due to the truncation can be
evaluated by approximating the reciprocal lattice sum for the excluded
contacts in Eq. (4.21) to an integral in the 3-dimensional 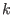 space and evaluating this integral from the cutoff
space and evaluating this integral from the cutoff
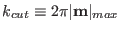 to infinity in polar coordinates. The neglected
reciprocal lattice intra-molecular energy is then [104]
to infinity in polar coordinates. The neglected
reciprocal lattice intra-molecular energy is then [104]
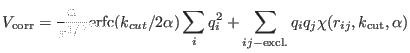 |
(4.44) |
with
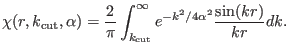 |
(4.45) |
The first constant term in (4.46) refers to the self energy,
while the second accounts for the intra-molecular excluded
interactions4.4.
This correction must be included in the same reference systems
to which
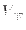 is assigned, e.g.
is assigned, e.g. 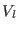 in our potential
separation (see Table 2).
in our potential
separation (see Table 2).
In principle the correction in Eq. (4.46) applies only to standard
Ewald and not to the reciprocal lattice energy computed
via SPME. We can still, however, use the correction
Eq. (4.46), if a spherical cutoff
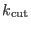 is applied to
SPME. This can be done easily by setting
is applied to
SPME. This can be done easily by setting
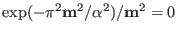 for
for
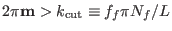 where
where 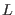 is the side length of the cubic box and
is the side length of the cubic box and
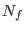 is the number of grid points in each direction. The factor
is the number of grid points in each direction. The factor
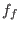 must be chosen slightly less than unity. This simple device
decreases the effective cutoff in reciprocal space while maintaining
the same grid spacing, thus reducing the B-spline interpolation error
(the error in the B-spline interpolation of the complex exponential
is, indeed, maximum precisely at the tail of the reciprocal sums
[35]). In Ref. [104] the effect of including
or not such correction in electrostatic systems using multiple time
step algorithms is studied and discussed thoroughly.
must be chosen slightly less than unity. This simple device
decreases the effective cutoff in reciprocal space while maintaining
the same grid spacing, thus reducing the B-spline interpolation error
(the error in the B-spline interpolation of the complex exponential
is, indeed, maximum precisely at the tail of the reciprocal sums
[35]). In Ref. [104] the effect of including
or not such correction in electrostatic systems using multiple time
step algorithms is studied and discussed thoroughly.
The potential
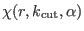 yields, in direct space,
the neglected reciprocal energy due to the truncation of the reciprocal
lattice sums, and must, in principle, be included for each atom pair
distance in direct space. Thus, the corrected direct space potential
is then
yields, in direct space,
the neglected reciprocal energy due to the truncation of the reciprocal
lattice sums, and must, in principle, be included for each atom pair
distance in direct space. Thus, the corrected direct space potential
is then
which is then split as usual in short-medium-long range according to
(4.39). The correction is certainly more crucial for the
excluded intramolecular contacts because
 is essentially a
short-ranged potential which is non negligible only for intramolecular
short distances. For systems with hydrogen bonds, however, the
correction is also important for intermolecular interactions.
is essentially a
short-ranged potential which is non negligible only for intramolecular
short distances. For systems with hydrogen bonds, however, the
correction is also important for intermolecular interactions.
In Fig. 4.4 the correction
potential is compared to the Coulomb potential (solid line in the top
right corner) for different value of the reciprocal space cutoff
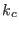 and of the convergence parameter
and of the convergence parameter 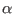 . For practical
values of
. For practical
values of 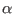 and
and 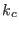 , the potential is short ranged and
small compared to the bare
, the potential is short ranged and
small compared to the bare 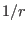 Coulomb interaction. In the asymptotic
limit
Coulomb interaction. In the asymptotic
limit 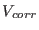 goes to zero as
goes to zero as
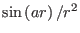 where
where 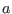 is a
constant. This oscillatory long range behavior of the correction
potential
is a
constant. This oscillatory long range behavior of the correction
potential
 is somewhat nasty: In Fig.
4.5 we show the integral
is somewhat nasty: In Fig.
4.5 we show the integral
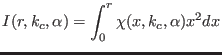 |
|
|
(4.47) |
as a function of the distance. If this integral converges then
the 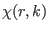 is absolutely convergent in 3D.
We see that the period of the oscillations in
is absolutely convergent in 3D.
We see that the period of the oscillations in 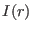 increases with
increases with
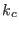 while
while 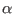 affects only the amplitude. The total energy
is hence again conditionally convergent, since the limit
affects only the amplitude. The total energy
is hence again conditionally convergent, since the limit
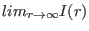 does not exist. However, unlike for
the
does not exist. However, unlike for
the 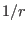 bare potential, the energy integral remains in this case
bounded. Due to this, a cutoff on the small potential
bare potential, the energy integral remains in this case
bounded. Due to this, a cutoff on the small potential
 is
certainly far less dangerous that a cutoff on the bare
is
certainly far less dangerous that a cutoff on the bare 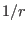 term.
In order to verify this, we have calculated some properties of liquid
water using the SPC model[105] from a 200 ps MD simulation in the
term.
In order to verify this, we have calculated some properties of liquid
water using the SPC model[105] from a 200 ps MD simulation in the
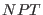 ensemble at temperature of 300 K and pressure of 0.1 MPa with i)
a very accurate Ewald sum (column EWALD in Table 4.2), ii) with inaccurate Ewald but
corrected in direct space using Eq. (4.48) (CORRECTED)
and iii) with simple cutoff truncation of the bare Coulomb potential
and no Ewald (CUTOFF). Results are reported in Table 4.2
ensemble at temperature of 300 K and pressure of 0.1 MPa with i)
a very accurate Ewald sum (column EWALD in Table 4.2), ii) with inaccurate Ewald but
corrected in direct space using Eq. (4.48) (CORRECTED)
and iii) with simple cutoff truncation of the bare Coulomb potential
and no Ewald (CUTOFF). Results are reported in Table 4.2
Table:
| |
EWALD |
CORRECTED |
CUTOFF |
| Coulomb energy (KJ/mole) |
-55.2 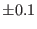 |
-55.1 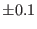 |
-56.4 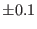 |
| Potential energy (KJ/mole) |
-46.2 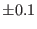 |
-46.1 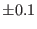 |
-47.3 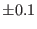 |
| Heat Capacity (KJ/mole/K) |
74 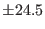 |
94 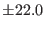 |
87 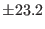 |
Volume (cm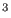 ) ) |
18.2 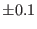 |
18.3 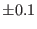 |
18.1 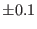 |
Volume Fluctuation (Å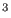 ) ) |
136.9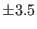 |
147.0 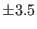 |
138.7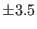 |
 (Å) (Å) |
2.81  |
2.81  |
2.81  |
| Dielectric constant |
59 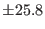 |
47 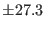 |
3 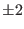 |
|
We notice that almost all the computed properties
of water are essentially independent, within statistical error, of the
truncation method. The dielectric properties, on the contrary, appear
very sensitive to the method for dealing with long range tails:
Accurate and inaccurate Ewald (corrected in direct space through
4.48) yields, within statistical error, comparable results
whereas the dielectric constant predicted by the spherical cutoff
method is more than order of magnitude smaller. We should remark that
method ii) (CORRECTED) is almost twice as efficient as the ``exact''
method i).
procacci
2021-12-29
![]() is applied to
SPME. This can be done easily by setting
is applied to
SPME. This can be done easily by setting
![]() for
for
![]() where
where ![]() is the side length of the cubic box and
is the side length of the cubic box and
![]() is the number of grid points in each direction. The factor
is the number of grid points in each direction. The factor
![]() must be chosen slightly less than unity. This simple device
decreases the effective cutoff in reciprocal space while maintaining
the same grid spacing, thus reducing the B-spline interpolation error
(the error in the B-spline interpolation of the complex exponential
is, indeed, maximum precisely at the tail of the reciprocal sums
[35]). In Ref. [104] the effect of including
or not such correction in electrostatic systems using multiple time
step algorithms is studied and discussed thoroughly.
must be chosen slightly less than unity. This simple device
decreases the effective cutoff in reciprocal space while maintaining
the same grid spacing, thus reducing the B-spline interpolation error
(the error in the B-spline interpolation of the complex exponential
is, indeed, maximum precisely at the tail of the reciprocal sums
[35]). In Ref. [104] the effect of including
or not such correction in electrostatic systems using multiple time
step algorithms is studied and discussed thoroughly.
![\includegraphics[scale=0.35]{alpha.eps}](img674.png)
![\includegraphics[scale=0.35]{kc.eps}](img675.png)
![]() and of the convergence parameter
and of the convergence parameter ![]() . For practical
values of
. For practical
values of ![]() and
and ![]() , the potential is short ranged and
small compared to the bare
, the potential is short ranged and
small compared to the bare ![]() Coulomb interaction. In the asymptotic
limit
Coulomb interaction. In the asymptotic
limit ![]() goes to zero as
goes to zero as
![]() where
where ![]() is a
constant. This oscillatory long range behavior of the correction
potential
is a
constant. This oscillatory long range behavior of the correction
potential
![]() is somewhat nasty: In Fig.
4.5 we show the integral
is somewhat nasty: In Fig.
4.5 we show the integral
![\includegraphics[scale=0.35]{int-alpha.eps}](img684.png)
![\includegraphics[scale=0.35]{int-kc.eps}](img685.png)