The Crooks theorem
Recent development on non equilibrium thermodynamics have clarified
that the PMF along the given reaction coordinate 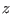 can actually be
reconstructed exactly using an ensemble of steered molecular
dynamics simulations without resorting to any assumption on, or having
any knowledge of the frictional behavior of the system along the
reaction coordinate. These developments date back to a paper by Evans,
Searls[146] where the first example of transient
fluctuation theorem for a system driven out of equilibrium was
formulated, demonstrating the connection between the time integral of
the phase compression factor in Liouville space along an arbitrary
time interval and the probability ratio of producing the entropy
can actually be
reconstructed exactly using an ensemble of steered molecular
dynamics simulations without resorting to any assumption on, or having
any knowledge of the frictional behavior of the system along the
reaction coordinate. These developments date back to a paper by Evans,
Searls[146] where the first example of transient
fluctuation theorem for a system driven out of equilibrium was
formulated, demonstrating the connection between the time integral of
the phase compression factor in Liouville space along an arbitrary
time interval and the probability ratio of producing the entropy 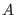 and
and 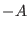 along a deterministic trajectory of a many particles non
equilibrium steady state system. Gavin Crooks in his phd thesis
proposed[64], in the context of Monte Carlo simulations in
the canonical ensemble (NVT), a transient[146]
fluctuation formula (from now on indicated with CT) involving the
dissipative work for systems driven out of equilibrium by varying some
arbitrary mechanical parameter. The CT is actually even more general
than the Evans and Searls fluctuation theorem[146] since in
the latter the driven
along a deterministic trajectory of a many particles non
equilibrium steady state system. Gavin Crooks in his phd thesis
proposed[64], in the context of Monte Carlo simulations in
the canonical ensemble (NVT), a transient[146]
fluctuation formula (from now on indicated with CT) involving the
dissipative work for systems driven out of equilibrium by varying some
arbitrary mechanical parameter. The CT is actually even more general
than the Evans and Searls fluctuation theorem[146] since in
the latter the driven 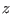 coordinate has an underlying zero PMF
(i.e. only entropy is produced in the non equilibrium process) while
in the former the system can also cross
different thermodynamics states (i.e. the underlying PMF can also
be non zero such that thermodynamic work can also be done). The Crooks
theorem (CT) reads
coordinate has an underlying zero PMF
(i.e. only entropy is produced in the non equilibrium process) while
in the former the system can also cross
different thermodynamics states (i.e. the underlying PMF can also
be non zero such that thermodynamic work can also be done). The Crooks
theorem (CT) reads
![$\displaystyle \frac{p(\Gamma(z_0) \rightarrow \Gamma(z_\tau))}{p(\Gamma^\ast(z_...
...)} = \exp [ \beta ( W_{\Gamma(z_0) \rightarrow \Gamma(z_\tau )} - \Delta F ) ],$](img1045.png) |
(8.2) |
where 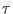 is the duration time of the driven non equilibrium
process,
is the duration time of the driven non equilibrium
process,
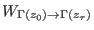 is the work done
on the system during the driven trajectory
is the work done
on the system during the driven trajectory
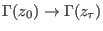 ;
;
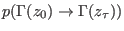 is the
joint probability of taking the microstate
is the
joint probability of taking the microstate
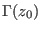 from a
canonical distribution with a given initial Hamiltonian
from a
canonical distribution with a given initial Hamiltonian 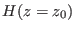 and
of performing the forward transformation to the microstate
and
of performing the forward transformation to the microstate
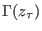 corresponding to a different Hamiltonian
corresponding to a different Hamiltonian
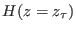 ;
;
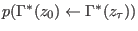 is
the analogous joint probability for the time reversal path,
producing the work
is
the analogous joint probability for the time reversal path,
producing the work
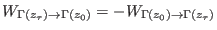 .
.
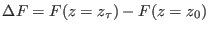 is the free energy difference between the thermodynamic
states associated to the Hamiltonians
is the free energy difference between the thermodynamic
states associated to the Hamiltonians
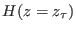 and
and 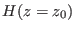 .
Although the CT can be stated in a more general formulation (see Gavin
Crooks,
.
Although the CT can be stated in a more general formulation (see Gavin
Crooks, 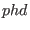 thesis), here the essential assumptions are that i) the
system is deterministic and satisfies the time reversal symmetry and
ii) the reverse trajectory is done following a reversed time
schedule such that
thesis), here the essential assumptions are that i) the
system is deterministic and satisfies the time reversal symmetry and
ii) the reverse trajectory is done following a reversed time
schedule such that
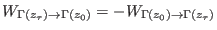 . The first assumption is
satisfied by any kind of standard MD equation of motion (Newtonian,
Nosé-Hoover. Parrinello-Rahman) while the second condition can be
easily imposed in a SMD experiment. A very simple proof of
Eq. 8.2 goes as follows: suppose the
. The first assumption is
satisfied by any kind of standard MD equation of motion (Newtonian,
Nosé-Hoover. Parrinello-Rahman) while the second condition can be
easily imposed in a SMD experiment. A very simple proof of
Eq. 8.2 goes as follows: suppose the 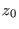 is drawn from
a canonical distribution, and that the driven trajectory that brings
the system to
is drawn from
a canonical distribution, and that the driven trajectory that brings
the system to 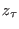 is done adiabatically, i.e. removing the
thermal bath. For the reverse trajectory, drawing
is done adiabatically, i.e. removing the
thermal bath. For the reverse trajectory, drawing 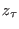 from a canonical
distribution, due to the time reversal symmetry of the Hamilton
equations, one ends up adiabatically in
from a canonical
distribution, due to the time reversal symmetry of the Hamilton
equations, one ends up adiabatically in 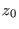 . Under these
assumptions, the ratio of the two probabilities on the left hand side
of Eq. 8.2 can be written as
. Under these
assumptions, the ratio of the two probabilities on the left hand side
of Eq. 8.2 can be written as
equation
where we have used the facts that
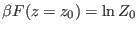 ,
,
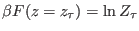 and that the energy difference
and that the energy difference 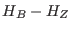 in
the forward adiabatic trajectory equals to the external work done on
the systems.
Equation 8.2 refers
to the probability of a single forward or backward trajectory.
Suppose now to perform a large number of forward trajectories all with
a give time schedule, but each started from a different initial phase
point sampled according to the canonical equilibrium distribution
characterized by the Hamiltonian
in
the forward adiabatic trajectory equals to the external work done on
the systems.
Equation 8.2 refers
to the probability of a single forward or backward trajectory.
Suppose now to perform a large number of forward trajectories all with
a give time schedule, but each started from a different initial phase
point sampled according to the canonical equilibrium distribution
characterized by the Hamiltonian 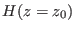 and a large and not
necessarily equal number of backward trajectories with reverse time
schedule and starting from initial phase points this time sampled
according to the canonical equilibrium distribution characterized by
the Hamiltonian
and a large and not
necessarily equal number of backward trajectories with reverse time
schedule and starting from initial phase points this time sampled
according to the canonical equilibrium distribution characterized by
the Hamiltonian 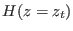 .8.2. By collecting all
trajectories yielding the work
.8.2. By collecting all
trajectories yielding the work 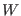 in (8.2), the CT may
compactly be written as:
in (8.2), the CT may
compactly be written as:
![$\displaystyle \frac{P_F(W)}{P_R(-W)} = \exp[ \beta (W - \Delta F) ],$](img1071.png) |
(8.4) |
where 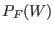 and
and 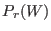 are the normalized forward and backward
distribution functions (note that, due to the time reversal symmetry,
for the backward distribution the work is taken with the minus sign,
i.e.
are the normalized forward and backward
distribution functions (note that, due to the time reversal symmetry,
for the backward distribution the work is taken with the minus sign,
i.e. 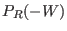 is the mirror symmetric with respect to
is the mirror symmetric with respect to 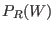 ).
According to Eq. 8.4, the
).
According to Eq. 8.4, the 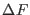 may be thus evaluated
constructing the two work distribution function:
may be thus evaluated
constructing the two work distribution function: 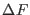 is the
work value where the two distribution cross, i.e
is the
work value where the two distribution cross, i.e
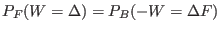 .
We point out in passing that, the famous Jarzynski
identity[63] (JI),
.
We point out in passing that, the famous Jarzynski
identity[63] (JI),
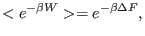 |
(8.5) |
is actually a trivial consequence of the CT, being derived from the
latter by integrating out the work variable and using the fact that
the work distribution function 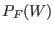 and
and 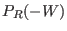 are normalized.
are normalized.
The physical meaning of the Crooks equation sounds indeed very
reasonable and can be even be considered as a probabilistic restatement
of the second law or of a generalization of the H-Boltzmann theorem:
Given a forward deterministic non equilibrium trajectory
starting form equilibrium and producing a work 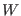 , the probability to
observe a trajectory for the reverse process again starting from
equilibrium and producing the work
, the probability to
observe a trajectory for the reverse process again starting from
equilibrium and producing the work 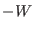 is
is
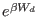 small than
the former, where
small than
the former, where
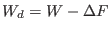 is the dissipated work in the
forward process. When the dissipated work is zero, i.e. when the
driven process is quasi-static and is done always at equilibrium,
then the two probabilities are identical. With this regard, one
important point to stress is that the CT and the JI hold for all
systems and for any kind of arbitrary non equilibrium process, no matter how fast is performed. In particular, if the non
equilibrium process is instantaneous, i.e. if it is done at
infinite speed, then the work done on the system is simply equal to
is the dissipated work in the
forward process. When the dissipated work is zero, i.e. when the
driven process is quasi-static and is done always at equilibrium,
then the two probabilities are identical. With this regard, one
important point to stress is that the CT and the JI hold for all
systems and for any kind of arbitrary non equilibrium process, no matter how fast is performed. In particular, if the non
equilibrium process is instantaneous, i.e. if it is done at
infinite speed, then the work done on the system is simply equal to
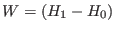 , with
, with 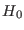 and
and 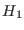 being the Hamiltonian of the
initial and final state, respectively. The JI reduces in this case to
the to famous free energy perturbation Zwanzig[119] formula
being the Hamiltonian of the
initial and final state, respectively. The JI reduces in this case to
the to famous free energy perturbation Zwanzig[119] formula
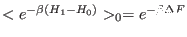 with the subscript 0
indicating that the canonical average must be taken according to the
equilibrium distribution of the system with Hamiltonian
with the subscript 0
indicating that the canonical average must be taken according to the
equilibrium distribution of the system with Hamiltonian 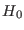 .
.
For fast non equilibrium experiments, a large amount of the work,
rather than in advancing the reaction coordinate, is dissipated
in heat that is in turn (only partly) assimilated by the thermal
bath8.3 A consequence of this is that the
maxima of two work distributions 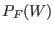 and
and 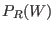 tend to get
further apart from each other so that the determination of
tend to get
further apart from each other so that the determination of 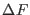 becomes less accurate. The faster are performed the non equilibrium
experiments, the large is the average dissipation and the smaller is
the overlap between the two work distributions (see Fig.
8.1)
The reason why CT and JI can be so useful in evaluating the free
energies along given reaction paths in the molecular dynamics
simulation of complex biological system lies on the fact that this
methodologies are inherently more accurate the smaller is the
sample. Let's see why. As one can see form Fig. 8.1,
becomes less accurate. The faster are performed the non equilibrium
experiments, the large is the average dissipation and the smaller is
the overlap between the two work distributions (see Fig.
8.1)
The reason why CT and JI can be so useful in evaluating the free
energies along given reaction paths in the molecular dynamics
simulation of complex biological system lies on the fact that this
methodologies are inherently more accurate the smaller is the
sample. Let's see why. As one can see form Fig. 8.1, 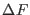 can be determined with accuracy if the two work distributions
overlap appreciably, or stated in other terms, if there are sufficient
trajectories that in both directions transiently violate the second
law, i.e trajectories for which
can be determined with accuracy if the two work distributions
overlap appreciably, or stated in other terms, if there are sufficient
trajectories that in both directions transiently violate the second
law, i.e trajectories for which
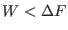 . This is clearly not in
contrast with the second law which states that
. This is clearly not in
contrast with the second law which states that
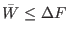 where
where
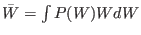 is the mean irreversible work.
In general, the probability of an overlap of the two work
distributions (i.e. the probability of transiently violating the
second law) is clearly larger the smaller is the system.
is the mean irreversible work.
In general, the probability of an overlap of the two work
distributions (i.e. the probability of transiently violating the
second law) is clearly larger the smaller is the system.
Suppose to
simultaneously and irreversibly unfold 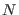 identical proteins in
a dilute solution starting from their native states. In the assumption
that the intraprotein interaction are negligible, the mean work for
this system will be simply
identical proteins in
a dilute solution starting from their native states. In the assumption
that the intraprotein interaction are negligible, the mean work for
this system will be simply 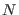 times the mean work done on a single molecule, while the width of the work distribution for the
times the mean work done on a single molecule, while the width of the work distribution for the
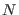 molecule systems will be only
molecule systems will be only 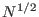 larger than that of the
single molecule system. This effect is illustrated in
Fig. 8.2. Now, biomolecular simulation of biosystems are
usually done, for computational reasons, on a single solvated
biomolecule, i.e. in the conditions where the non equilibrium
techniques, for the reason explained above, are deemed to be more
successful.
larger than that of the
single molecule system. This effect is illustrated in
Fig. 8.2. Now, biomolecular simulation of biosystems are
usually done, for computational reasons, on a single solvated
biomolecule, i.e. in the conditions where the non equilibrium
techniques, for the reason explained above, are deemed to be more
successful.
procacci
2021-12-29
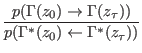
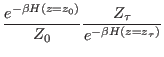
![\includegraphics[width=7.0cm,height=5.6cm]{smd.eps}](img1066.png)
![\includegraphics[width=7.0cm,height=5.6cm]{smd2.eps}](img1067.png)
![]() , the probability to
observe a trajectory for the reverse process again starting from
equilibrium and producing the work
, the probability to
observe a trajectory for the reverse process again starting from
equilibrium and producing the work ![]() is
is
![]() small than
the former, where
small than
the former, where
![]() is the dissipated work in the
forward process. When the dissipated work is zero, i.e. when the
driven process is quasi-static and is done always at equilibrium,
then the two probabilities are identical. With this regard, one
important point to stress is that the CT and the JI hold for all
systems and for any kind of arbitrary non equilibrium process, no matter how fast is performed. In particular, if the non
equilibrium process is instantaneous, i.e. if it is done at
infinite speed, then the work done on the system is simply equal to
is the dissipated work in the
forward process. When the dissipated work is zero, i.e. when the
driven process is quasi-static and is done always at equilibrium,
then the two probabilities are identical. With this regard, one
important point to stress is that the CT and the JI hold for all
systems and for any kind of arbitrary non equilibrium process, no matter how fast is performed. In particular, if the non
equilibrium process is instantaneous, i.e. if it is done at
infinite speed, then the work done on the system is simply equal to
![]() , with
, with ![]() and
and ![]() being the Hamiltonian of the
initial and final state, respectively. The JI reduces in this case to
the to famous free energy perturbation Zwanzig[119] formula
being the Hamiltonian of the
initial and final state, respectively. The JI reduces in this case to
the to famous free energy perturbation Zwanzig[119] formula
![]() with the subscript 0
indicating that the canonical average must be taken according to the
equilibrium distribution of the system with Hamiltonian
with the subscript 0
indicating that the canonical average must be taken according to the
equilibrium distribution of the system with Hamiltonian ![]() .
.
![]() and
and ![]() tend to get
further apart from each other so that the determination of
tend to get
further apart from each other so that the determination of ![]() becomes less accurate. The faster are performed the non equilibrium
experiments, the large is the average dissipation and the smaller is
the overlap between the two work distributions (see Fig.
8.1)
The reason why CT and JI can be so useful in evaluating the free
energies along given reaction paths in the molecular dynamics
simulation of complex biological system lies on the fact that this
methodologies are inherently more accurate the smaller is the
sample. Let's see why. As one can see form Fig. 8.1,
becomes less accurate. The faster are performed the non equilibrium
experiments, the large is the average dissipation and the smaller is
the overlap between the two work distributions (see Fig.
8.1)
The reason why CT and JI can be so useful in evaluating the free
energies along given reaction paths in the molecular dynamics
simulation of complex biological system lies on the fact that this
methodologies are inherently more accurate the smaller is the
sample. Let's see why. As one can see form Fig. 8.1, ![]() can be determined with accuracy if the two work distributions
overlap appreciably, or stated in other terms, if there are sufficient
trajectories that in both directions transiently violate the second
law, i.e trajectories for which
can be determined with accuracy if the two work distributions
overlap appreciably, or stated in other terms, if there are sufficient
trajectories that in both directions transiently violate the second
law, i.e trajectories for which
![]() . This is clearly not in
contrast with the second law which states that
. This is clearly not in
contrast with the second law which states that
![]() where
where
![]() is the mean irreversible work.
In general, the probability of an overlap of the two work
distributions (i.e. the probability of transiently violating the
second law) is clearly larger the smaller is the system.
is the mean irreversible work.
In general, the probability of an overlap of the two work
distributions (i.e. the probability of transiently violating the
second law) is clearly larger the smaller is the system.
![\includegraphics[width=7.0cm,height=5.6cm]{smd.eps}](img1066.png)
![\includegraphics[width=7.0cm,height=5.6cm]{triple.eps}](img1089.png)