The Jarzynski identity is
seemingly a better route than the CT to evaluate the full potential of
mean force along 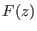 in the interval
in the interval ![$ [z_0,z_t]$](img1091.png) , with
, with 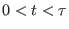 .
However the exponential averages in Eq. 8.5 is known to
be strongly biased, i.e. it contains a systematic error[149]
that grows with decreasing number of non equilibrium experiments. This
can be qualitatively explained with the fact that, for dissipative
fast non equilibrium experiments, the forward work distribution
.
However the exponential averages in Eq. 8.5 is known to
be strongly biased, i.e. it contains a systematic error[149]
that grows with decreasing number of non equilibrium experiments. This
can be qualitatively explained with the fact that, for dissipative
fast non equilibrium experiments, the forward work distribution 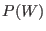 has its maximum where the exponential factor
has its maximum where the exponential factor
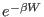 is
negligibly small, so that the size of the integrand
is
negligibly small, so that the size of the integrand
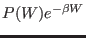 is de facto controlled by the left tail of the
is de facto controlled by the left tail of the 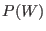 distribution.[65] An unfortunate consequence of this, is
that the PMF calculated through the JI becomes more and more biased as
the reaction
distribution.[65] An unfortunate consequence of this, is
that the PMF calculated through the JI becomes more and more biased as
the reaction 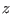 coordinate is advanced, since the accumulated
dissipation work shift the maximum of the
coordinate is advanced, since the accumulated
dissipation work shift the maximum of the 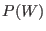 distribution
distribution
The CT is far more precise than the JI to evaluate free energy
differences. Shirts and Pande[66] have restated the CT
theorem showing that the maximum likelihood estimate (MLE) of the free
energy difference exactly correspond to the so-called Bennett
acceptance ratio[118]8.4. The MLE restatement
of the CT is the following
![$\displaystyle \sum_{i=1}^{n_F} \frac{1}{ 1 + \frac{n_F}{n_R} ~ {\rm e}^{ \beta ...
...1}{ 1 + \frac{n_R}{n_F} ~ {\rm e}^{ \beta (
W[{\mathbf R}_i] + \Delta F ) } } -$](img1096.png) |
|
|
(8.6) |
where the
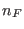 ,
, 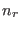 are the number of forward and backward non equilibrium
experiments and
are the number of forward and backward non equilibrium
experiments and
![$ W[{\mathbf F}_i]$](img1099.png)
![$ W[{\mathbf R}_i]$](img1100.png) indicate the
outcome of i-th forward and backward work measurement. This equation
has only one solution for
indicate the
outcome of i-th forward and backward work measurement. This equation
has only one solution for 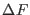 , i.e. the MLE. As such, however,
the Crooks theorem allows, through the MLE estimate based on
bidirectional work measurements, to compute the free energy difference
, i.e. the MLE. As such, however,
the Crooks theorem allows, through the MLE estimate based on
bidirectional work measurements, to compute the free energy difference
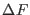 between the end points (i.e. between thermodynamic
states at fixed and given reaction coordinates
between the end points (i.e. between thermodynamic
states at fixed and given reaction coordinates 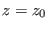 and
and
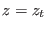 ). In principle, to reconstruct the full PMF along the reaction
coordinate
). In principle, to reconstruct the full PMF along the reaction
coordinate 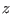 , in the spirit of thermodynamics integration, One
should provide a series of equilibrium ensembles of configurations at
intermediate values of
, in the spirit of thermodynamics integration, One
should provide a series of equilibrium ensembles of configurations at
intermediate values of 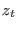 . Here, we briefly sketch out a
methodology for reconstructing the full PMF in the segment
. Here, we briefly sketch out a
methodology for reconstructing the full PMF in the segment
![$ [z_0,z_\tau]$](img1103.png) doing only the two work measurements from
doing only the two work measurements from 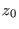 to
to
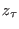 and back. We first rewrite the Crooks equation,
Eq. 8.2, as follows
and back. We first rewrite the Crooks equation,
Eq. 8.2, as follows
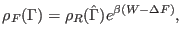 |
(8.7) |
where 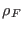 ,
, 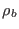 are the probability to
observe a particular trajectory
are the probability to
observe a particular trajectory 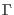 in the forward and reverse
process, respectively and
in the forward and reverse
process, respectively and
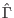 indicate the time trajectory
taken with inverted time schedule.
Eq. 8.7 trivially implies that
indicate the time trajectory
taken with inverted time schedule.
Eq. 8.7 trivially implies that
where
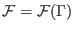 ,
,
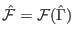 is an arbitrary functional of the trajectory
is an arbitrary functional of the trajectory
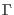 and of its inverted time schedule counterpart
and of its inverted time schedule counterpart
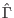 .
Using Eq. 8.7, we thus can combine the direct estimate of
.
Using Eq. 8.7, we thus can combine the direct estimate of
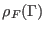 with the indirect estimate of the same quantity obtained
from
with the indirect estimate of the same quantity obtained
from
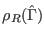 . This latter, according to
Eq. 8.7, must be unbiased with the weight factor
corresponding to the exponential of the dissipated work in the forward
measurement. If the direct and indirect (Eq. 8.7) estimates are done with
. This latter, according to
Eq. 8.7, must be unbiased with the weight factor
corresponding to the exponential of the dissipated work in the forward
measurement. If the direct and indirect (Eq. 8.7) estimates are done with 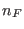 forward measurements and
forward measurements and 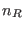 reverse measurements, respectively, the
optimal (minimum variance) combination of these two estimates of
reverse measurements, respectively, the
optimal (minimum variance) combination of these two estimates of
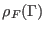 is done according to the WHAM
formula[54]
is done according to the WHAM
formula[54]
Here W is the work done in the full
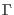 path from the end point at
path from the end point at 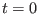 to the end point at
to the end point at
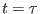 . We now calculate the average of the trajectory functional
. We now calculate the average of the trajectory functional
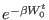 at intermediate times
at intermediate times
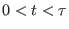 , using the
optimized above density. Taking the average of this functional over
forward (
, using the
optimized above density. Taking the average of this functional over
forward (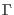 ) and reverse (
) and reverse (
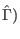 work measurements,
exploiting the Jarzynski identity 8.5 in the form
work measurements,
exploiting the Jarzynski identity 8.5 in the form
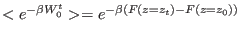 , using the
fact that
, using the
fact that 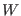 is odd under time reversal and that
is odd under time reversal and that
![$ W_0^t[\hat \Gamma]=
-W^\tau_{(\tau-t)}[\Gamma]$](img1124.png) , we obtain the following estimate for the
free energy at intermediate
, we obtain the following estimate for the
free energy at intermediate 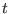 , with
, with 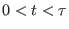 :
:
This equation, due to Minh and Adib[125], allows to
reconstruct the entire potential of mean force 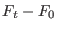 along the reaction coordinate
spanned during the bidirectional non equilibrium experiments of duration
along the reaction coordinate
spanned during the bidirectional non equilibrium experiments of duration
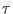 , no matter how fast the driven processes are done.
Note that
, no matter how fast the driven processes are done.
Note that
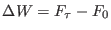 and
and 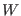 in Eq. 8.11 are the
forward free energy difference and work relative the end points,
respectively.
in Eq. 8.11 are the
forward free energy difference and work relative the end points,
respectively.
For fast pulling experiments, i.e. when the dissipated work is large,
it can be shown[150], that Eq. 8.11 reduces to
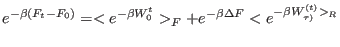 |
(8.12) |
In both Eq. 8.12 and Eq. 8.11 one needs to know the
free energy difference between the end points 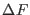 . An unbiased
estimate of
. An unbiased
estimate of 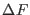 is easily available through the Bennett acceptance ratio,
Eq. 8.6.
is easily available through the Bennett acceptance ratio,
Eq. 8.6.
procacci
2021-12-29
![]() in the interval
in the interval ![]() , with
, with ![]() .
However the exponential averages in Eq. 8.5 is known to
be strongly biased, i.e. it contains a systematic error[149]
that grows with decreasing number of non equilibrium experiments. This
can be qualitatively explained with the fact that, for dissipative
fast non equilibrium experiments, the forward work distribution
.
However the exponential averages in Eq. 8.5 is known to
be strongly biased, i.e. it contains a systematic error[149]
that grows with decreasing number of non equilibrium experiments. This
can be qualitatively explained with the fact that, for dissipative
fast non equilibrium experiments, the forward work distribution ![]() has its maximum where the exponential factor
has its maximum where the exponential factor
![]() is
negligibly small, so that the size of the integrand
is
negligibly small, so that the size of the integrand
![]() is de facto controlled by the left tail of the
is de facto controlled by the left tail of the ![]() distribution.[65] An unfortunate consequence of this, is
that the PMF calculated through the JI becomes more and more biased as
the reaction
distribution.[65] An unfortunate consequence of this, is
that the PMF calculated through the JI becomes more and more biased as
the reaction ![]() coordinate is advanced, since the accumulated
dissipation work shift the maximum of the
coordinate is advanced, since the accumulated
dissipation work shift the maximum of the ![]() distribution
distribution
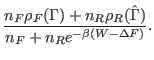
![]() along the reaction coordinate
spanned during the bidirectional non equilibrium experiments of duration
along the reaction coordinate
spanned during the bidirectional non equilibrium experiments of duration
![]() , no matter how fast the driven processes are done.
Note that
, no matter how fast the driven processes are done.
Note that
![]() and
and ![]() in Eq. 8.11 are the
forward free energy difference and work relative the end points,
respectively.
in Eq. 8.11 are the
forward free energy difference and work relative the end points,
respectively.