Implementation in ORAC
Steered molecular dynamics in ORAC is implemented by adding an
external driving potential depending on user defined internal
coordinates in the form of stretching, bending, torsions. The general
form of the time dependent external potential that bring the system
from an initial state at 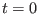 to a different final state
to a different final state 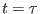 is
given by
is
given by
where 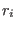 ,
, 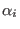 and
and 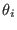 represents the actual
represents the actual 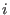 -th
stretching , bending and torsional driven coordinate defined by
arbitrarily selecting in the corresponding input definition the
involved atoms. So a driven torsion or a stretching may be defined
using arbitrarily chosen atoms of the solute that are not connected
by any real bond.
-th
stretching , bending and torsional driven coordinate defined by
arbitrarily selecting in the corresponding input definition the
involved atoms. So a driven torsion or a stretching may be defined
using arbitrarily chosen atoms of the solute that are not connected
by any real bond. 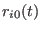 ,
,
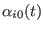 and
and
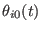 are time dependent parameters that defines the non equilibrium
trajectory in the space of the coordinates. In ORAC , each of these
parameters, given the duration
are time dependent parameters that defines the non equilibrium
trajectory in the space of the coordinates. In ORAC , each of these
parameters, given the duration 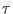 of the non equilibrium
experiment, is varied at constant speed from an initial value at
time
of the non equilibrium
experiment, is varied at constant speed from an initial value at
time 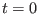 defining the reactants, to a final value at time
defining the reactants, to a final value at time 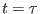 defining the products :
defining the products :
As all the steering velocities are constant during the experiments,
the above equations define a line
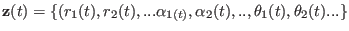 |
(8.15) |
in a reaction coordinate space at
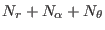 dimensions
dimensions
The work done by the external potential, Eq. 8.13, in
the time 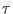 of the non equilibrium driven process along the
coordinate
of the non equilibrium driven process along the
coordinate 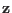 is calculated as
is calculated as
The equilibrium distribution of the starting points for independent work
measurements can be
determined (either by a standard equilibrium molecular dynamics
simulation or by some enhanced simulation technique) by constraining
the system with the harmonic constraint
for the reactants' state and
for the products' state. Having produced the work in a series of
bidirectional experiments, one can then either apply the Bennett
formula. Eq. 8.6, to compute the free energy
differences between the reactants and the products states, or, using
the intermediate work values 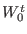 , apply Eq. 8.11 or
Eq. 8.12 to reconstruct the entire potential of mean force
along the the mono-dimensional driven trajectory in a multidimensional
reaction coordinate space defined in Eq. 8.14. In order to
define a non necessarily linear trajectory in a multidimensional
reaction coordinate space (e.g. a putative minimum free energy path),
on must be able to assign to a each steered coordinate a different
steering time protocol. This can be done in ORAC by providing an
auxiliary file defining the path in coordinate space. The file has the
general form shown in Table 8.3.
, apply Eq. 8.11 or
Eq. 8.12 to reconstruct the entire potential of mean force
along the the mono-dimensional driven trajectory in a multidimensional
reaction coordinate space defined in Eq. 8.14. In order to
define a non necessarily linear trajectory in a multidimensional
reaction coordinate space (e.g. a putative minimum free energy path),
on must be able to assign to a each steered coordinate a different
steering time protocol. This can be done in ORAC by providing an
auxiliary file defining the path in coordinate space. The file has the
general form shown in Table 8.3.
Table:
General format of the file defining of an arbitrary time protocol for a curvilinear path
in a reaction coordinates space at
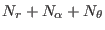 dimensions in ORAC . For a
generic coordinate
dimensions in ORAC . For a
generic coordinate
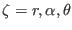 , the steering velocity
between times
, the steering velocity
between times 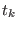 and
and 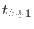 is constant and equal to
is constant and equal to
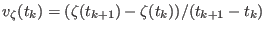
 |
 |
... |
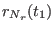 |
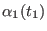 |
... |
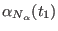 |
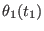 |
... |
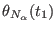 |
|
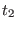 |
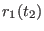 |
... |
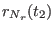 |
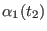 |
... |
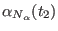 |
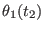 |
... |
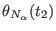 |
|
| |
... |
... |
... |
|
|
|
|
|
|
|
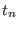 |
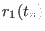 |
... |
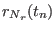 |
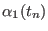 |
... |
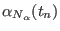 |
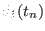 |
... |
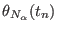 |
|
|
|
|
|
|
|
|
|
|
|
|
|
The free energy or potential of mean force obtained with the described
protocols are not depurated by the jacobian terms arising form the
definition of the reaction coordinates. For example, the potential of
mean force, calculated with Eq. 8.11 or Eq. 8.12 along a
driven distance for a freely rotating object includes the additional contribution
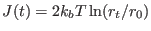 arising from
the fact that the configurational probability
arising from
the fact that the configurational probability 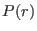 , for two non
interacting particles grows with the square of the distance. Moreover
the PMF calculated using the driving potential given in
Eq. 8.13 are in principle affected by the so-called stiff
spring approximation,[148] i.e. if the constant
, for two non
interacting particles grows with the square of the distance. Moreover
the PMF calculated using the driving potential given in
Eq. 8.13 are in principle affected by the so-called stiff
spring approximation,[148] i.e. if the constant
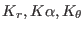 in Eq. 8.13 are not large enough, then one
actually computes the free energy associated to the Hamiltonian
in Eq. 8.13 are not large enough, then one
actually computes the free energy associated to the Hamiltonian
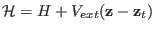 rather than that associated to the
Hamiltonian
rather than that associated to the
Hamiltonian
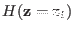 . However the impact of the
strength of the force constant on the computed non equilibrium
average, especially if the reaction coordinate is characterized by
inherently slow dynamics and/or the underlying unbiased potential of
mean force is much less stiffer than the harmonic driving potential,
is generally rather small even at relatively low values of force
constant. With this respect, it has been shown that[148]
. However the impact of the
strength of the force constant on the computed non equilibrium
average, especially if the reaction coordinate is characterized by
inherently slow dynamics and/or the underlying unbiased potential of
mean force is much less stiffer than the harmonic driving potential,
is generally rather small even at relatively low values of force
constant. With this respect, it has been shown that[148]
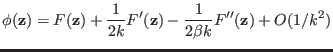 |
(8.19) |
where
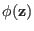 is PMF of the unbiased system with the
Hamiltonian
is PMF of the unbiased system with the
Hamiltonian
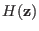 , while
, while
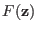 is the PMF that is
actually measured in the SMD experiments, i.e. that corresponding to
the biased Hamiltonian
is the PMF that is
actually measured in the SMD experiments, i.e. that corresponding to
the biased Hamiltonian
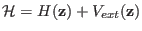 . From Eq. 8.19, one sees that if the derivatives of
. From Eq. 8.19, one sees that if the derivatives of
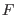 are not too high or
are not too high or 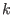 is chosen large enough, then one can
safely assume that
is chosen large enough, then one can
safely assume that
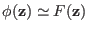 .
.
eq:intraq:intra1
procacci
2021-12-29
![]() of the non equilibrium driven process along the
coordinate
of the non equilibrium driven process along the
coordinate ![]() is calculated as
is calculated as