Alchemical Transformations
In the following we shall describe in details the theory of continuous
alchemical transformations, with focus on the issues and
technicalities regarding the implementation in molecular dynamics code
using the Ewald method. As we will see, running a simulation using
standard implementation of the Ewald methods of a system where atomic
charges are varying, implies the insurgence of non trivial terms in
the energy and forces that must be considered for producing correct
trajectories. In a nutshell, Ewald resummations consists in adding
and subtracting to the atomic point charges a spherical Gaussian
charge distributions bearing the same charge, so that the
electrostatic potential is split in a fast dying term (the Erfc
term), due to the sum of the point charge and the neutralizing charge
distribution and evaluated in the direct lattice, and in a slowly
decaying term (the Erf term) due to the added Gaussian spherical
distributions evaluated in the reciprocal
lattice. Thanks to this trick, the conditionally convergent
electrostatic energy sum is split in two absolutely convergent
series. In standard implementations of the Ewald resummation
technique, as we will see later on, the electrostatic potential at the
atomic position 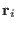 is actually not available with mixing of
the interactions between alchemical and non alchemical species in the
so-called Ewald reciprocal lattice contribution (i.e. the Erf
part). The Smooth Particle Mesh Ewald method (see
Chapter 3) makes no exception, with
the additional complication that the atomic point charges (including
the alchemical charges) are now smeared over nearby grid points to
produce a regularly gridded charge distribution, to be evaluated using
Fast Fourier Transform (FFT). Due to the extraordinary efficiency
(see Figure 4.3),
the Particle Mesh Ewald method is still an unrivaled methodology for
the evaluation of electrostatic interactions in complex
systems. Moreover, PME can be straightforwardly
incorporated in fast multiple time step schemes producing extremely
efficient algorithms for, e.g., systems of biological
interest. For these reasons, it is therefore highly
desirable to devise rigorous and efficient approaches to account for
alchemical effects in a system treated with PME.
is actually not available with mixing of
the interactions between alchemical and non alchemical species in the
so-called Ewald reciprocal lattice contribution (i.e. the Erf
part). The Smooth Particle Mesh Ewald method (see
Chapter 3) makes no exception, with
the additional complication that the atomic point charges (including
the alchemical charges) are now smeared over nearby grid points to
produce a regularly gridded charge distribution, to be evaluated using
Fast Fourier Transform (FFT). Due to the extraordinary efficiency
(see Figure 4.3),
the Particle Mesh Ewald method is still an unrivaled methodology for
the evaluation of electrostatic interactions in complex
systems. Moreover, PME can be straightforwardly
incorporated in fast multiple time step schemes producing extremely
efficient algorithms for, e.g., systems of biological
interest. For these reasons, it is therefore highly
desirable to devise rigorous and efficient approaches to account for
alchemical effects in a system treated with PME.
Subsections
procacci
2021-12-29