The work done on the system by the driven alchemical coordinates
during a simulation of length 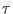 can be written as
can be written as
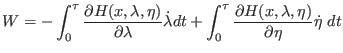 |
(9.7) |
In a NVT or NPT extended Lagrangian simulation with an ongoing alchemical process, the
alchemical work, Eq. 9.7, could be computed simply by monitoring
the changes in the total energy of the systems, that includes
the real potential and kinetic energy of system and the potential and
kinetic energies of the barostat and the thermostats. This energy, if
no velocity scaling is implemented (i.e. no heat is artificially transferred to or
absorbed from the extended system), is a constant of the motion and hence any
variation of it must correspond to the work done on the
system.[155] Alternatively the work can be computed by
analytically evaluating the 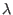 and
and 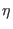 derivatives of the
non bonded energy Eq. 9.6. Both these methods have
counter-indications. The total energy method suffers form the finite
precision of energy conservation in the numerical integration of the
equations of motion (usually in multiple time step schemes the
oscillations of the total energy are
the order of 1/50:1/100 of the mean fluctuation of the potential energy of
the system)[13]. Also, small drifts in the total energy
adds up in the work as a spurious extra dissipation term that may reduce
the accuracy in the free energy determination via the Crooks
theorem. The method based the derivatives, if alchemical species are
annihilated and created within the same process, requires the constant
tagging of the two creation and annihilation works, as the
increments
derivatives of the
non bonded energy Eq. 9.6. Both these methods have
counter-indications. The total energy method suffers form the finite
precision of energy conservation in the numerical integration of the
equations of motion (usually in multiple time step schemes the
oscillations of the total energy are
the order of 1/50:1/100 of the mean fluctuation of the potential energy of
the system)[13]. Also, small drifts in the total energy
adds up in the work as a spurious extra dissipation term that may reduce
the accuracy in the free energy determination via the Crooks
theorem. The method based the derivatives, if alchemical species are
annihilated and created within the same process, requires the constant
tagging of the two creation and annihilation works, as the
increments
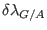 or
or
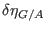 have
opposite signs for creation (
have
opposite signs for creation (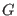 species) and
annihilation process (
species) and
annihilation process (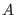 species). Besides, while all direct lattice Erfc and
and reciprocal lattice Erf corrections terms pose no difficulties in
species). Besides, while all direct lattice Erfc and
and reciprocal lattice Erf corrections terms pose no difficulties in 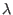 derivation with a moderate
extra cost of the force routines, the analytic derivation of
reciprocal lattice energy
derivation with a moderate
extra cost of the force routines, the analytic derivation of
reciprocal lattice energy
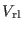 , Eq. 9.2, with respect to
, Eq. 9.2, with respect to 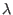 implies the calculation
of three gridded charge arrays, i.e. one for the whole system and two
more for the discharging and for the charging alchemical solutes:
implies the calculation
of three gridded charge arrays, i.e. one for the whole system and two
more for the discharging and for the charging alchemical solutes:
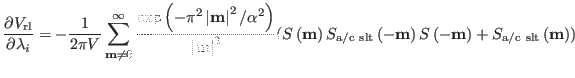 |
(9.8) |
where with the notation
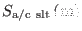 we refer to the
gridded charge arrays obtained for the discharging (
we refer to the
gridded charge arrays obtained for the discharging (
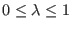 ) and charging alchemical species (
) and charging alchemical species (
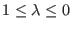 )
if they are both present.
)
if they are both present.
The work can also by computed numerically observing that the
differential work due to a
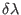 or
or
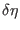 increment
of the alchemical factors is given by
increment
of the alchemical factors is given by
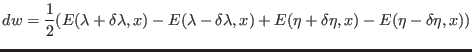 |
(9.9) |
which is correct to order
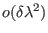 and
and
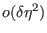 . Eq. 9.9 requires just one extra calculation of the
energy within the direct space force loop using the
. Eq. 9.9 requires just one extra calculation of the
energy within the direct space force loop using the 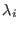 values at the previous step with no need for tagging annihilating and
creating species. For computing the work arising from the reciprocal
lattice sum, Eq. 9.2, the gridded charge array must be
computed at every step of the intermediate-range shell using the
current charges and those at the previous step with a very limited
computational cost. Both these array must then undergo FFT. As
for the direct lattice, also for the reciprocal term there is no need
for tagging creating or annihilating species. The different means to
access the alchemical work can be used as a powerful check to test
the coherency of the trajectories and of the computed numerical work,
Eq. 9.9. The alchemical work indirectly evaluated
monitoring the changes of total energy of the system, must follow
closely the profile of the numerical work computed using
Eq. 9.9. Such test is reported in Figure 9.2
(right) for the discharging of ethanol in water.
values at the previous step with no need for tagging annihilating and
creating species. For computing the work arising from the reciprocal
lattice sum, Eq. 9.2, the gridded charge array must be
computed at every step of the intermediate-range shell using the
current charges and those at the previous step with a very limited
computational cost. Both these array must then undergo FFT. As
for the direct lattice, also for the reciprocal term there is no need
for tagging creating or annihilating species. The different means to
access the alchemical work can be used as a powerful check to test
the coherency of the trajectories and of the computed numerical work,
Eq. 9.9. The alchemical work indirectly evaluated
monitoring the changes of total energy of the system, must follow
closely the profile of the numerical work computed using
Eq. 9.9. Such test is reported in Figure 9.2
(right) for the discharging of ethanol in water.
In a multiple time step
scheme, the alchemical work must be computed exactly as the energy is
computed, hence evaluating more often the contributions arising from
the fast shells with respect to the terms evolving more slowly. In
the scheme reported in the Supporting Information, we succinctly the
describe the implementation of the alchemical process and the
associated work calculation in a molecular dynamics code, highlighting
the parts of the code that must be modified because of the
presence of alchemical species with respect to a normal MD code.
Figure:
Left: Time record for the intrasolute reciprocal lattice
contributions to the differential work (Eq. 9.9) arising
form electrostatic interactions during the alchemical discharging of
ethanol in water at T=300 K and P=1 Atm. The simulation went on for
15 ps. The red curve is due the self term
![$ -\frac{\alpha}{\pi^{1/2}}\sum_i [1-\lambda_i(t)]^2Q_i^2$](img1230.png) . The green
curve is due to the direct lattice contribution and to
. The green
curve is due to the direct lattice contribution and to
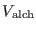 . The magenta curve includes the terms
. The magenta curve includes the terms
 (Eq. 9.4). The blue curve is due to the full reciprocal
lattice PME term, Eq. 9.2. Right: Total energy change (red
line) and numerical work (black line) computed using
Eq. 9.9 for the
discharging of ethanol in water in an alchemical trajectory lasting
for 9 ps.
(Eq. 9.4). The blue curve is due to the full reciprocal
lattice PME term, Eq. 9.2. Right: Total energy change (red
line) and numerical work (black line) computed using
Eq. 9.9 for the
discharging of ethanol in water in an alchemical trajectory lasting
for 9 ps.
![\includegraphics[scale=0.34,clip]{Figures_alchemy/work.eps}](img1246.png)
![\includegraphics[scale=0.34,clip]{Figures_alchemy/work_check.eps}](img1247.png) |
In Figure 9.2 we report the behavior of the various
contributions to the intra-solute differential work computed during the
transformation. In the reciprocal lattice term (blue curve) the
intrasolute and solute-solvent contributions are mixed. Hence
the integrated total differential work (black curve) is, expectedly, slightly positive
due to loss of long-range electrostatic energy because of ethanol
discharging. Again, paralleling the situation seen for the intrasolute
energy, the work due to the self term approximately cancels the end
Erfc intrasolute contributions.
We conclude this section with some comments on the time protocol that
drives the alchemical transformation. In our implementation, the
charges and the Lennard-Jones potential can be switched on and off
independently, by setting up different time protocol for 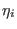 and
and
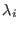 alchemical coordinates. Such as approach is much more
flexible and powerful than that based on the definition of a single
alchemical parameter implying the simultaneous variation of Lennard-Jones
and electrostatic interactions. If the
alchemical coordinates. Such as approach is much more
flexible and powerful than that based on the definition of a single
alchemical parameter implying the simultaneous variation of Lennard-Jones
and electrostatic interactions. If the 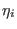 and
and 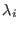 factors are varied
coherently (i.e. only one type of alchemical coordinate
factors are varied
coherently (i.e. only one type of alchemical coordinate
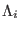 is defined), catastrophic numerical instabilities may
arise, especially in complex solutes with competing conformational
structures. One way to circumvent this
problem is to switch electrostatic and Lennard-Jones interactions
separately as we do here.
is defined), catastrophic numerical instabilities may
arise, especially in complex solutes with competing conformational
structures. One way to circumvent this
problem is to switch electrostatic and Lennard-Jones interactions
separately as we do here.
For the evaluation of solvation free
energy via alchemical transformations, the target end states are i)
the decoupled solute (in the gas phase) and the pure solvent (in the
liquid state) and ii) the solution. For the decoupled state i), in
principle two independent standard simulations are needed, one for the
isolated solute and the other for pure solvent. However the decoupled
state can be sampled in one single simulation using the non-bonded
energy of Eq. 9.6, by setting the alchemical solute
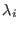 and
and 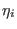 factors all equal to one. In fact, according to
Eq. 9.6 and to the rules of Table 9.1, when the
alchemical solute
factors all equal to one. In fact, according to
Eq. 9.6 and to the rules of Table 9.1, when the
alchemical solute 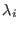 and
and 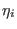 terms are all equal to one,
the solute is not felt by any means by the solvent and evolves in time
independently, subject only to the intramolecular interactions with no
contribution form the solute lattice images. The intrasolute
electrostatic energy, in particular, has no contribution from the
reciprocal lattice sum as the
terms are all equal to one,
the solute is not felt by any means by the solvent and evolves in time
independently, subject only to the intramolecular interactions with no
contribution form the solute lattice images. The intrasolute
electrostatic energy, in particular, has no contribution from the
reciprocal lattice sum as the 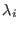 referring to the solute are
all equal to 1 in Eq. 9.2. It has indeed a direct lattice
contribution for non bonded intrasolute evaluated in the zero cell
according to the rules specified in Table 9.1 plus
the alchemic correction term that simply corresponds (with all solute
referring to the solute are
all equal to 1 in Eq. 9.2. It has indeed a direct lattice
contribution for non bonded intrasolute evaluated in the zero cell
according to the rules specified in Table 9.1 plus
the alchemic correction term that simply corresponds (with all solute
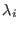 set to 1) to the complementary Erf part thus recovering
the bare intrasolute Coulomb energy. At the other extreme end of the alchemical
transformation (
set to 1) to the complementary Erf part thus recovering
the bare intrasolute Coulomb energy. At the other extreme end of the alchemical
transformation (
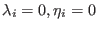 ), according to
Eq. 9.6 the solute is fully
charged interacting normally with the solvent and with the solute images via
the term Eq. 9.2
), according to
Eq. 9.6 the solute is fully
charged interacting normally with the solvent and with the solute images via
the term Eq. 9.2
Figure 9.3:
Alchemical work produced in the creation of ethanol
in water T=300 K and P=1 Atm using two different time protocols represented by the black and red horizontal lines.
![\includegraphics[scale=0.60,clip]{Figures_alchemy/gapsys.eps}](img1250.png) |
We now come to the issue of the efficiency of a code with distinct
Lennard-Jones and charge alchemical parameters. Of course, also in
this case simultaneous switching of 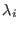 and
and 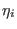 remains
perfectly possible. To avoid numerical instabilities at the early
stage of the creation process or at the end of the annihilation, it is
sufficient in the first case to slightly delay the charge switching
and in last case to anticipate the discharging process. In the Figure
9.3 we report the work computed in the alchemical
creation of ethanol in water conducted with two different time
protocol. In the red non equilibrium trajectory, the Lennard-Jones
remains
perfectly possible. To avoid numerical instabilities at the early
stage of the creation process or at the end of the annihilation, it is
sufficient in the first case to slightly delay the charge switching
and in last case to anticipate the discharging process. In the Figure
9.3 we report the work computed in the alchemical
creation of ethanol in water conducted with two different time
protocol. In the red non equilibrium trajectory, the Lennard-Jones
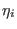 parameters for ethanol are prudently brought from 1 to 0 in
30 ps, and in the next 20 ps the solute is charged. In the black
trajectories lasting for 30 ps, in the first 10 ps, the
parameters for ethanol are prudently brought from 1 to 0 in
30 ps, and in the next 20 ps the solute is charged. In the black
trajectories lasting for 30 ps, in the first 10 ps, the 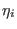 coordinates alone are brought from 1 to 0.5 and then, in the last 20 ps, they are brought
to zero (fully switched on ethanol) together with the charging
process that is started at 10 ps. As one can see, both trajectories
are regular with no instabilities, yielding negative and comparable
works with limited dissipation with respect to the reversible work (
16-17 kJ mol
coordinates alone are brought from 1 to 0.5 and then, in the last 20 ps, they are brought
to zero (fully switched on ethanol) together with the charging
process that is started at 10 ps. As one can see, both trajectories
are regular with no instabilities, yielding negative and comparable
works with limited dissipation with respect to the reversible work (
16-17 kJ mol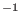 , see next section) in spite of short duration of
the non equilibrium alchemical transformations. We must stress here,
that in the fast switching non equilibrium method with determination
of the free energy difference between end states via the CFT, once the
equilibrium configurations of the starting end states have been
prepared, the simulation time per trajectory does correspond indeed to
the wall-clock time if the independent non-equilibrium trajectories are
performed in parallel. For the creation of ethanol in water, the CPU
time amounts to few minutes on a low-end Desktop computer for both
time protocols.
, see next section) in spite of short duration of
the non equilibrium alchemical transformations. We must stress here,
that in the fast switching non equilibrium method with determination
of the free energy difference between end states via the CFT, once the
equilibrium configurations of the starting end states have been
prepared, the simulation time per trajectory does correspond indeed to
the wall-clock time if the independent non-equilibrium trajectories are
performed in parallel. For the creation of ethanol in water, the CPU
time amounts to few minutes on a low-end Desktop computer for both
time protocols.
In the following scheme, we succinctly describe the implementation of
alchemical transformations in a MD driver code with multiple time step (MTS)
integrators and Particle Mesh Ewald treatment of long range
electrostatics in ORAC. The modification due the alchemical
transformations are highlighted in red.
Alchemical MD pseudo-code





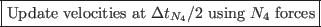
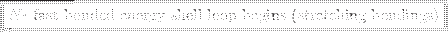















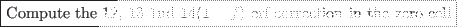
![\framebox{\textcolor{red}{Subtract the self energy $\frac{\alpha}{\pi^{1/2}}\sum_i [1-\lambda_i(t)]^2q_i$}}](img1279.png)

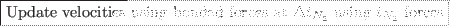





The computational overhead after the inclusion of the
alchemical code in the MD driver is mostly due to the evaluation of
the alchemical work during the non equilibrium driven experiment. As
the simulation proceeds, the alchemical work must be computed in the
direct lattice as well as in the reciprocal lattice with a frequency
identical to that of the energy terms. For the reciprocal lattice
contribution, one extra Fast Fourier Transform is required in order to
evaluate the reciprocal lattice Particle Mesh Ewald energy at the
previous step. Moreover, the Erf correction
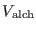 (Eq. 9.5) is an entirely new energy term due to the
alchemical species. The efficiency loss of the alchemical code with
respect to a non alchemical code is around 30%, as measured in a
short serial simulation of ethanol in water in standard conditions
(see Methods section of the main paper for the simulation parameters),
(Eq. 9.5) is an entirely new energy term due to the
alchemical species. The efficiency loss of the alchemical code with
respect to a non alchemical code is around 30%, as measured in a
short serial simulation of ethanol in water in standard conditions
(see Methods section of the main paper for the simulation parameters),
procacci
2021-12-29
![]() or
or
![]() increment
of the alchemical factors is given by
increment
of the alchemical factors is given by
![\includegraphics[scale=0.34,clip]{Figures_alchemy/work.eps}](img1246.png)
![\includegraphics[scale=0.34,clip]{Figures_alchemy/work_check.eps}](img1247.png)
![]() and
and
![]() alchemical coordinates. Such as approach is much more
flexible and powerful than that based on the definition of a single
alchemical parameter implying the simultaneous variation of Lennard-Jones
and electrostatic interactions. If the
alchemical coordinates. Such as approach is much more
flexible and powerful than that based on the definition of a single
alchemical parameter implying the simultaneous variation of Lennard-Jones
and electrostatic interactions. If the ![]() and
and ![]() factors are varied
coherently (i.e. only one type of alchemical coordinate
factors are varied
coherently (i.e. only one type of alchemical coordinate
![]() is defined), catastrophic numerical instabilities may
arise, especially in complex solutes with competing conformational
structures. One way to circumvent this
problem is to switch electrostatic and Lennard-Jones interactions
separately as we do here.
is defined), catastrophic numerical instabilities may
arise, especially in complex solutes with competing conformational
structures. One way to circumvent this
problem is to switch electrostatic and Lennard-Jones interactions
separately as we do here.
![]() and
and ![]() factors all equal to one. In fact, according to
Eq. 9.6 and to the rules of Table 9.1, when the
alchemical solute
factors all equal to one. In fact, according to
Eq. 9.6 and to the rules of Table 9.1, when the
alchemical solute ![]() and
and ![]() terms are all equal to one,
the solute is not felt by any means by the solvent and evolves in time
independently, subject only to the intramolecular interactions with no
contribution form the solute lattice images. The intrasolute
electrostatic energy, in particular, has no contribution from the
reciprocal lattice sum as the
terms are all equal to one,
the solute is not felt by any means by the solvent and evolves in time
independently, subject only to the intramolecular interactions with no
contribution form the solute lattice images. The intrasolute
electrostatic energy, in particular, has no contribution from the
reciprocal lattice sum as the ![]() referring to the solute are
all equal to 1 in Eq. 9.2. It has indeed a direct lattice
contribution for non bonded intrasolute evaluated in the zero cell
according to the rules specified in Table 9.1 plus
the alchemic correction term that simply corresponds (with all solute
referring to the solute are
all equal to 1 in Eq. 9.2. It has indeed a direct lattice
contribution for non bonded intrasolute evaluated in the zero cell
according to the rules specified in Table 9.1 plus
the alchemic correction term that simply corresponds (with all solute
![]() set to 1) to the complementary Erf part thus recovering
the bare intrasolute Coulomb energy. At the other extreme end of the alchemical
transformation (
set to 1) to the complementary Erf part thus recovering
the bare intrasolute Coulomb energy. At the other extreme end of the alchemical
transformation (
![]() ), according to
Eq. 9.6 the solute is fully
charged interacting normally with the solvent and with the solute images via
the term Eq. 9.2
), according to
Eq. 9.6 the solute is fully
charged interacting normally with the solvent and with the solute images via
the term Eq. 9.2
![\includegraphics[scale=0.60,clip]{Figures_alchemy/gapsys.eps}](img1250.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Eq. 9.5) is an entirely new energy term due to the
alchemical species. The efficiency loss of the alchemical code with
respect to a non alchemical code is around 30%, as measured in a
short serial simulation of ethanol in water in standard conditions
(see Methods section of the main paper for the simulation parameters),
(Eq. 9.5) is an entirely new energy term due to the
alchemical species. The efficiency loss of the alchemical code with
respect to a non alchemical code is around 30%, as measured in a
short serial simulation of ethanol in water in standard conditions
(see Methods section of the main paper for the simulation parameters),