Temperature REM
The Replica Exchange Method is based on
multiple concurrent (parallel) canonical simulation that are allowed
to occasionally exchange their configurations. For a system made of
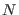 atoms,
by ``configuration'' we mean a state defined by a
atoms,
by ``configuration'' we mean a state defined by a 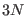 dimensional
coordinate vector, independent of the momenta. Thus, in a
replica exchange, only coordinates and not momenta are exchanged. In
the standard implementation of the methodology, each replica, bearing
a common interaction potential, is characterized by a given
temperature and configurations between couple of replicas are
tentatively exchanged at prescribed time intervals using a
probabilistic criterion. The target temperature, i.e. the
temperature corresponding to the thermodynamic state of interest, is
usually the lowest among all replicas. In this manner, ``hot''
configurations from hot replicas, i.e. configurations where energy
barrier are easily crossed, may be occasionally accepted at the target
temperature. The canonical
probability of a coordinate configuration
dimensional
coordinate vector, independent of the momenta. Thus, in a
replica exchange, only coordinates and not momenta are exchanged. In
the standard implementation of the methodology, each replica, bearing
a common interaction potential, is characterized by a given
temperature and configurations between couple of replicas are
tentatively exchanged at prescribed time intervals using a
probabilistic criterion. The target temperature, i.e. the
temperature corresponding to the thermodynamic state of interest, is
usually the lowest among all replicas. In this manner, ``hot''
configurations from hot replicas, i.e. configurations where energy
barrier are easily crossed, may be occasionally accepted at the target
temperature. The canonical
probability of a coordinate configuration 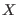 for
for  -th replica is
given by
-th replica is
given by
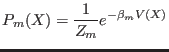 |
(5.1) |
where  is the replica index,
is the replica index,
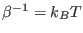 ,
, 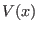 is the
potential of the system, and
is the
potential of the system, and
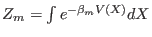 is the configurational partition function for
is the configurational partition function for  -th replica. Being the
-th replica. Being the
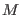 replicas independent, the probability distribution for a
generic configuration of the
replicas independent, the probability distribution for a
generic configuration of the 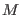 -fold extended system
-fold extended system
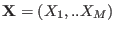 is
is
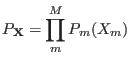 |
(5.2) |
As stated above, the global state 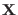 of the extended system may
evolve in two ways: i) by evolving each replica independently
(i.e. via MC or MD simulation protocols) and ii) by exchanging the
configurations of two replicas. Regarding the second mechanism, we introduce
the transition probability
of the extended system may
evolve in two ways: i) by evolving each replica independently
(i.e. via MC or MD simulation protocols) and ii) by exchanging the
configurations of two replicas. Regarding the second mechanism, we introduce
the transition probability
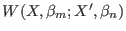 for the exchange between
the configuration
for the exchange between
the configuration 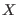 of replica at
of replica at 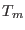 and the configuration
and the configuration
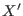 for the replica
for the replica 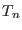 . The probability for the inverse
exchange is clearly given by
. The probability for the inverse
exchange is clearly given by
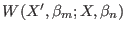 .
The detailed balance condition on the extended system for this kind of
moves is given by
.
The detailed balance condition on the extended system for this kind of
moves is given by
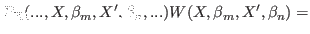 |
|
|
(5.3) |
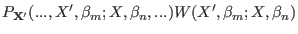 |
|
|
(5.4) |
which, using the expressions 5.2 and 5.1 for the global probability,
is satisfied if the transition probability satisfies the equation
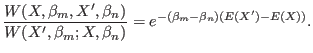 |
(5.5) |
The exchange of configurations of replicas obeying the detailed balance condition 5.5
can be as usual implemented by using the Metropolis algorithm
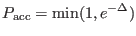 |
(5.6) |
with
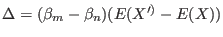 . Like in a
standard MC technique, because of the detailed balance condition for
the extended system, the sampling in the
. Like in a
standard MC technique, because of the detailed balance condition for
the extended system, the sampling in the  multi-configuration space
in REM evolves towards a global equilibrium defined by
the multi-canonical probability distribution of the extended system
Eq. 5.2.
multi-configuration space
in REM evolves towards a global equilibrium defined by
the multi-canonical probability distribution of the extended system
Eq. 5.2.
In principle Eq. 5.6 refers to the probability of an
exchange between any two replicas. In practice the exchanges are
attempted between replicas that are contiguous in temperature. Let's
see why. For any two replicas  ,
,  , the total number of accepted
exchanges between them is given by
, the total number of accepted
exchanges between them is given by
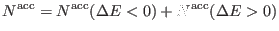 |
(5.7) |
where
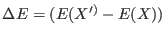 and
and
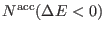 ,
,
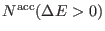 are the number of accepted exchanges
for which
are the number of accepted exchanges
for which
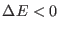 and
and
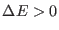 , respectively.
When the extended system is at equilibrium, we clearly must have that
, respectively.
When the extended system is at equilibrium, we clearly must have that
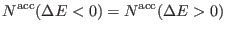 |
(5.8) |
Inserting the above equation into Eq. 5.7, we obtain
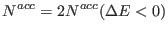 |
(5.9) |
Since, according to the prescription 5.6, the
probability for accepting the move when
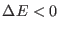 is unitary, we
may write that
is unitary, we
may write that
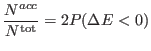 |
(5.10) |
where
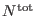 is the total number of attempted exchanges and
is the total number of attempted exchanges and
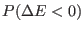 is the cumulative probability that a
is the cumulative probability that a
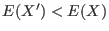 .
Eq. 5.10 states that if the two normalized
(configurational) energy distribution
.
Eq. 5.10 states that if the two normalized
(configurational) energy distribution 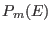 of replica
of replica  and
and
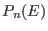 of replica
of replica  are identical, then the probability for a
successful exchange between the two replica is equal to the area of the
overlap of the two distribution (i.e. the shaded area in Fig. 5.1). If
are identical, then the probability for a
successful exchange between the two replica is equal to the area of the
overlap of the two distribution (i.e. the shaded area in Fig. 5.1). If
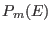 and
and 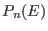 are not identical, we have in general that the
overlap of the two distribution is a lower bound for the acceptance
probability (the standard deviation
are not identical, we have in general that the
overlap of the two distribution is a lower bound for the acceptance
probability (the standard deviation
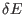 generally increases with the mean energy
generally increases with the mean energy 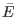 ).
Based on the above, and assuming that
).
Based on the above, and assuming that 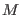 , the total number of
replicas, is even, one can then set up an exchange protocol
periodically attempting
, the total number of
replicas, is even, one can then set up an exchange protocol
periodically attempting 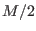 simultaneous contiguous replica exchanges
simultaneous contiguous replica exchanges
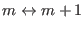 with
with  odd, or
odd, or 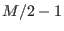 simultaneous
contiguous replica exchanges
simultaneous
contiguous replica exchanges
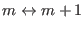 with
with  even,
accepting each of them with probability given by
5.6.
even,
accepting each of them with probability given by
5.6.
Given the above scheme, what is the optimal spacing in temperatures
for enhanced sampling of the configuration space at the target
temperature? First of all, the hottest temperature 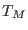 , defining
the full temperature range
, defining
the full temperature range
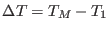 of the extended
system, must be clearly selected such that
of the extended
system, must be clearly selected such that 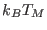 is of the order
of the maximum height of the free energy barriers that must be
overcome at the target temperature
is of the order
of the maximum height of the free energy barriers that must be
overcome at the target temperature 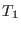 . Concerning the temperature
spacing, we have seen that acceptance probability for an exchange is
larger, the larger is the overlap of the two energy distributions
referring to the two contiguous replica, i.e. the closer are the
temperatures. Of course, the closer are the temperatures and the
larger is the number of replicas to be simulated, i.e. the heavier is
the CPU cost of the simulation. For an optimal choice, we thus set
. Concerning the temperature
spacing, we have seen that acceptance probability for an exchange is
larger, the larger is the overlap of the two energy distributions
referring to the two contiguous replica, i.e. the closer are the
temperatures. Of course, the closer are the temperatures and the
larger is the number of replicas to be simulated, i.e. the heavier is
the CPU cost of the simulation. For an optimal choice, we thus set
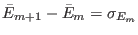 |
(5.11) |
where
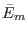 and
and
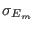 are the mean energy and the
standard deviation of energy distribution for the
are the mean energy and the
standard deviation of energy distribution for the  -the replica.
Assuming then that the system can be described by an ensemble of
-the replica.
Assuming then that the system can be described by an ensemble of 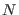 harmonic oscillators, we have that
harmonic oscillators, we have that
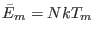 and
and
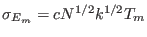 .5.1 Substituting these values in
Eq. 5.11, we obtain the temperature spacing for optimal
superposition:
.5.1 Substituting these values in
Eq. 5.11, we obtain the temperature spacing for optimal
superposition:
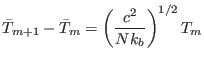 |
(5.12) |
In the parallel implementation of the temperature REM, in order to
keep the communication overhead at the lowest possible level, we standardly
exchange the temperatures and not the configurations. So the  -th
slave process may explore the entire range of temperatures.
When the
-th
slave process may explore the entire range of temperatures.
When the  -th slave process periodically writes out the coordinates
of the configuration (Typically in pdb or xyz format), one must also
keep track of the current temperature (the program does this
automatically) in order be able to reconstruct a posteriori the
true
-th slave process periodically writes out the coordinates
of the configuration (Typically in pdb or xyz format), one must also
keep track of the current temperature (the program does this
automatically) in order be able to reconstruct a posteriori the
true  -th temperature configurational space of the
-th temperature configurational space of the  -th replica.
In Fig. 5.2, we show a typical parallel REM simulation
for a general system with 8 processes. In the x-axis we report the
simulation time, in the left y-axis the process index and in the right
y-axis the replica index which is bound to the actual
temperature. Each color represents a process running in parallel with
other processes with different colors. As it can be seen, on each
process the temperature (i.e. the replica index) changes
continuously.. So, for example the configurational sampling of the
replica at the lowest temperature in the given time interval must be
reconstructed combining the data for the slave processes 1,2,3,4,6 If
the algorithm is working properly, (i.e. if the temperature spacing is
chosen correctly and if there are no phase transition between
-th replica.
In Fig. 5.2, we show a typical parallel REM simulation
for a general system with 8 processes. In the x-axis we report the
simulation time, in the left y-axis the process index and in the right
y-axis the replica index which is bound to the actual
temperature. Each color represents a process running in parallel with
other processes with different colors. As it can be seen, on each
process the temperature (i.e. the replica index) changes
continuously.. So, for example the configurational sampling of the
replica at the lowest temperature in the given time interval must be
reconstructed combining the data for the slave processes 1,2,3,4,6 If
the algorithm is working properly, (i.e. if the temperature spacing is
chosen correctly and if there are no phase transition between 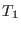 and
and 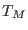 ), the temperature in each parallel process must perform a
random walk in the temperature domain
), the temperature in each parallel process must perform a
random walk in the temperature domain ![$ [T_1,T_M]$](img752.png) .
.
Going back to equation 5.12, two important issues must be
stressed: i) the temperature spacing for optimal overlap between
contiguous replicas while keeping the total number of replicas not too
high, is not uniform but grows with the replica temperature; ii) the
temperature spacing between contiguous replicas must be decreased with
increasing number of degrees of freedom. The latter is indeed a
severe limitation of the standard REM technology, since, as the size
of the system grows, a larger number of replicas must be employed for
preserving a significant exchange acceptance probability. This is
due to the inescapable fact that the energy fluctuations grow with
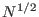 while the energy grows with
while the energy grows with 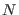 . Moreover, in many
important cases, one has to effectively samples reaction coordinates
that are rather localized in the protein, like e.g. in the case of
substrate-active site interactions. In the standard temperature REM,
the extra heat in the hot replicas is clearly distributed among all the degrees of freedom of the system and therefore most
of this heat is uselessly used for exchanging uninteresting
configurations (e.g. solvent configurations).
. Moreover, in many
important cases, one has to effectively samples reaction coordinates
that are rather localized in the protein, like e.g. in the case of
substrate-active site interactions. In the standard temperature REM,
the extra heat in the hot replicas is clearly distributed among all the degrees of freedom of the system and therefore most
of this heat is uselessly used for exchanging uninteresting
configurations (e.g. solvent configurations).
procacci
2021-12-29
![]() ,
, ![]() , the total number of accepted
exchanges between them is given by
, the total number of accepted
exchanges between them is given by
![\includegraphics[scale=.55,clip]{gaussian.eps}](img730.png)
![]() , defining
the full temperature range
, defining
the full temperature range
![]() of the extended
system, must be clearly selected such that
of the extended
system, must be clearly selected such that ![]() is of the order
of the maximum height of the free energy barriers that must be
overcome at the target temperature
is of the order
of the maximum height of the free energy barriers that must be
overcome at the target temperature ![]() . Concerning the temperature
spacing, we have seen that acceptance probability for an exchange is
larger, the larger is the overlap of the two energy distributions
referring to the two contiguous replica, i.e. the closer are the
temperatures. Of course, the closer are the temperatures and the
larger is the number of replicas to be simulated, i.e. the heavier is
the CPU cost of the simulation. For an optimal choice, we thus set
. Concerning the temperature
spacing, we have seen that acceptance probability for an exchange is
larger, the larger is the overlap of the two energy distributions
referring to the two contiguous replica, i.e. the closer are the
temperatures. Of course, the closer are the temperatures and the
larger is the number of replicas to be simulated, i.e. the heavier is
the CPU cost of the simulation. For an optimal choice, we thus set
![\includegraphics[scale=.55,clip]{traiettoriarepliche2.eps}](img751.png)
![]() while the energy grows with
while the energy grows with ![]() . Moreover, in many
important cases, one has to effectively samples reaction coordinates
that are rather localized in the protein, like e.g. in the case of
substrate-active site interactions. In the standard temperature REM,
the extra heat in the hot replicas is clearly distributed among all the degrees of freedom of the system and therefore most
of this heat is uselessly used for exchanging uninteresting
configurations (e.g. solvent configurations).
. Moreover, in many
important cases, one has to effectively samples reaction coordinates
that are rather localized in the protein, like e.g. in the case of
substrate-active site interactions. In the standard temperature REM,
the extra heat in the hot replicas is clearly distributed among all the degrees of freedom of the system and therefore most
of this heat is uselessly used for exchanging uninteresting
configurations (e.g. solvent configurations).