Fundamentals of serial generalized-ensemble methods
SGE methods deal with a set of 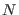 ensembles associated with different
dimensionless Hamiltonians
ensembles associated with different
dimensionless Hamiltonians 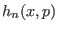 , where
, where 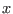 and
and 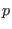 denote the
atomic coordinates and momenta of a microstate6.1, and
denote the
atomic coordinates and momenta of a microstate6.1, and
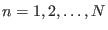 denotes the ensemble. Each ensemble is
characterized by a partition function expressed as
denotes the ensemble. Each ensemble is
characterized by a partition function expressed as
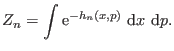 |
(6.1) |
In ST simulations we have temperature ensembles and therefore the
dimensionless Hamiltonian is
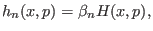 |
(6.2) |
where 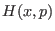 is the original Hamiltonian and
is the original Hamiltonian and
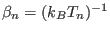 , with
, with 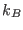 being the Boltzmann constant and
being the Boltzmann constant and 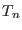 the
temperature of the
the
temperature of the  th ensemble. If we express the Hamiltonian as a
function of
th ensemble. If we express the Hamiltonian as a
function of 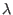 , namely a parameter correlated with an arbitrary
collective coordinate of the system (or even corresponding to the
pressure), then the dimensionless Hamiltonian associated with the
, namely a parameter correlated with an arbitrary
collective coordinate of the system (or even corresponding to the
pressure), then the dimensionless Hamiltonian associated with the
 th
th 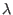 -ensemble is
-ensemble is
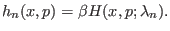 |
(6.3) |
Here all ensembles have the same temperature. It is also possible to
construct a generalized ensemble for multiple
parameters[120] as
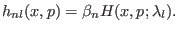 |
(6.4) |
In this example two parameters, 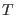 and
and 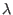 , are
employed. However no restraint is actually given to the number of
ensemble-spaces. Generalized-ensemble algorithms have a different
implementation dependent on whether the temperature is included in the
collection of sampling spaces (Eqs. 6.2 and
6.4) or not (Eq. 6.3). Here we adhere to
the most general context without specifying any form of
, are
employed. However no restraint is actually given to the number of
ensemble-spaces. Generalized-ensemble algorithms have a different
implementation dependent on whether the temperature is included in the
collection of sampling spaces (Eqs. 6.2 and
6.4) or not (Eq. 6.3). Here we adhere to
the most general context without specifying any form of 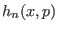 .
.
In SGE simulations, the probability of a microstate 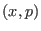 in the
in the
 th ensemble [from now on denoted as
th ensemble [from now on denoted as 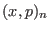 ] is proportional to
] is proportional to
![$ \exp[ -h_n(x,p) + g_n]$](img847.png) , where
, where 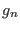 is a factor, different for each
ensemble, that must ensure almost equal visitation of the
is a factor, different for each
ensemble, that must ensure almost equal visitation of the 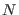 ensembles. The extended partition function of this ``system of
ensembles'' is
ensembles. The extended partition function of this ``system of
ensembles'' is
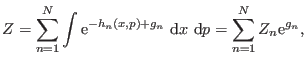 |
(6.5) |
where 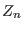 is the partition function of the system in the
is the partition function of the system in the  th
ensemble (Eq. 6.1). In practice, SGE simulations work as
follows. A single simulation is performed in a specific ensemble, say
th
ensemble (Eq. 6.1). In practice, SGE simulations work as
follows. A single simulation is performed in a specific ensemble, say
 , using Monte Carlo or molecular dynamics sampling protocols, and
after a certain interval, an attempt is made to change the microstate
, using Monte Carlo or molecular dynamics sampling protocols, and
after a certain interval, an attempt is made to change the microstate
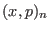 to another microstate of a different ensemble,
to another microstate of a different ensemble,
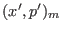 . Since high acceptance rates are obtained as the
ensembles
. Since high acceptance rates are obtained as the
ensembles  and
and  overlap significantly, the final ensemble
overlap significantly, the final ensemble  is
typically close to the initial one, namely
is
typically close to the initial one, namely
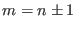 6.2. In principle, the
initial and final microstates can be defined by different coordinates
and/or momenta (
6.2. In principle, the
initial and final microstates can be defined by different coordinates
and/or momenta (
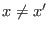 and/or
and/or
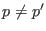 ), though the
condition
), though the
condition
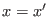 is usually adopted. The transition
probabilities for moving from
is usually adopted. The transition
probabilities for moving from 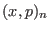 to
to
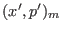 and vice versa have to satisfy the detailed balance condition
and vice versa have to satisfy the detailed balance condition
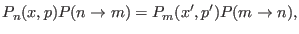 |
(6.6) |
where 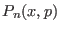 is the probability of the microstate
is the probability of the microstate 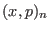 in the
extended canonical ensemble (Eq. 6.5)
in the
extended canonical ensemble (Eq. 6.5)
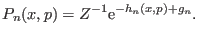 |
(6.7) |
In Eq. 6.6,
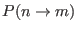 is a shorthand
for the conditional probability of the transition
is a shorthand
for the conditional probability of the transition
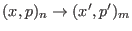 , given the system is in the microstate
, given the system is in the microstate
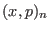 [with analogous meaning of
[with analogous meaning of
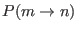 ]. Using
Eq. 6.7 together with the analogous expression for
]. Using
Eq. 6.7 together with the analogous expression for
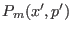 in the detailed balance and applying the
Metropolis's criterion, we find that the transition
in the detailed balance and applying the
Metropolis's criterion, we find that the transition
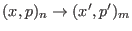 is accepted with probability
is accepted with probability
![$\displaystyle {\rm acc}[n \rightarrow m] = \min(1, {\rm e}^{h_n(x, p) - h_m(x^\prime, p^\prime) + g_m - g_n}).$](img864.png) |
(6.8) |
The probability of sampling a given ensemble is
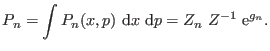 |
(6.9) |
Uniform sampling sets the condition
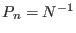 for each ensemble
(
for each ensemble
(
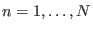 ), that leads to the equality
), that leads to the equality
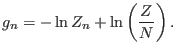 |
(6.10) |
Equation 6.10 implies that, to get uniform sampling, the
difference 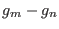 in Eq. 6.8 must be replaced
with
in Eq. 6.8 must be replaced
with 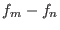 , where
, where 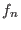 is the dimensionless free energy related
to the actual free energy of the ensemble
is the dimensionless free energy related
to the actual free energy of the ensemble  by the relation
by the relation
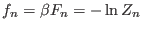 , where
, where 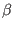 is the inverse temperature of the
ensemble. Here we are interested in determining such free energy
differences that will be referred as optimal weight factors, or
simply, optimal weights. Accordingly, in the acceptance ratio we will
use
is the inverse temperature of the
ensemble. Here we are interested in determining such free energy
differences that will be referred as optimal weight factors, or
simply, optimal weights. Accordingly, in the acceptance ratio we will
use 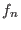 instead of
instead of 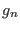 .
.
Subsections
procacci
2021-12-29
![]() ensembles associated with different
dimensionless Hamiltonians
ensembles associated with different
dimensionless Hamiltonians ![]() , where
, where ![]() and
and ![]() denote the
atomic coordinates and momenta of a microstate6.1, and
denote the
atomic coordinates and momenta of a microstate6.1, and
![]() denotes the ensemble. Each ensemble is
characterized by a partition function expressed as
denotes the ensemble. Each ensemble is
characterized by a partition function expressed as
![]() in the
in the
![]() th ensemble [from now on denoted as
th ensemble [from now on denoted as ![]() ] is proportional to
] is proportional to
![]() , where
, where ![]() is a factor, different for each
ensemble, that must ensure almost equal visitation of the
is a factor, different for each
ensemble, that must ensure almost equal visitation of the ![]() ensembles. The extended partition function of this ``system of
ensembles'' is
ensembles. The extended partition function of this ``system of
ensembles'' is