SGE simulations in temperature-space (simulated tempering)
and its implementation in the ORAC program
In SGE Monte Carlo simulations conducted in temperature-space (ST
simulations), Eq. 6.2 holds. Specifically, since only
configurational sampling is performed, we have
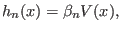 |
(6.11) |
where 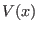 is the energy of the configuration
is the energy of the configuration 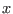 . Exploiting
Eq. 6.11 into Eq. 6.8, we find that
transitions from
. Exploiting
Eq. 6.11 into Eq. 6.8, we find that
transitions from  to
to  -ensemble, realized at fixed configuration,
are accepted with probability
-ensemble, realized at fixed configuration,
are accepted with probability
![$\displaystyle {\rm acc}[n \rightarrow m] = \min(1, {\rm e}^{( \beta_n - \beta_m) V(x) + f_m - f_n}).$](img875.png) |
(6.12) |
When the system evolution is performed with molecular dynamics
simulations, the situation is slightly more complicate. Suppose to
deal with canonical ensembles (to simplify the treatment and the
notation we consider constant-volume constant-temperature ensembles,
though extension to constant-pressure constant-temperature ensembles
is straightforward). Usually, constant temperature is implemented
through the Nosé-Hoover method[121,122] or
extensions of it[123]. With the symbol 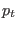 , we will
denote the momentum conjugated to the dynamical variable associated
with the thermostat. Also in this case Eq. 6.2 holds, but it
takes the form
, we will
denote the momentum conjugated to the dynamical variable associated
with the thermostat. Also in this case Eq. 6.2 holds, but it
takes the form
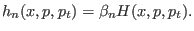 |
(6.13) |
In this equation,
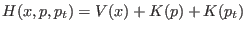 is the extended
Hamiltonian of the system, where
is the extended
Hamiltonian of the system, where 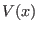 is the potential energy, while
is the potential energy, while
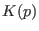 and
and 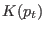 are the kinetic energies of the particles and
thermostat, respectively. As in Monte Carlo version, transitions from
are the kinetic energies of the particles and
thermostat, respectively. As in Monte Carlo version, transitions from
 to
to  -ensemble are realized at fixed configuration, while
particle momenta are rescaled as
-ensemble are realized at fixed configuration, while
particle momenta are rescaled as
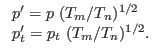 |
(6.14) |
As in temperature-REM[124], the scaling drops the momenta
out of the detailed balance and the acceptance ratio takes the form of
Eq. 6.12. Note that, if more thermostats are
adopted[123], then all additional momenta must be rescaled
according to Eq. 6.14.
ST is implemented in the ORAC program exactly as it has been done for
REM (see Section 5.2). In particular global and local
scalings of the potential energy can be realized by keeping fixed the
temperature of the system. A generic ensemble  is therefore defined
by a coefficient
is therefore defined
by a coefficient
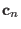 (see Eq. 5.13) that
scales the potential energy
(see Eq. 5.13) that
scales the potential energy
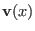 of the replica (the
vectorial form of the potential energy
of the replica (the
vectorial form of the potential energy 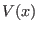 is used because of
possible local scaling), i.e.,
is used because of
possible local scaling), i.e.,
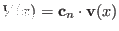 . In this sort of Hamiltonian tempering, the transition from
. In this sort of Hamiltonian tempering, the transition from
 to
to  -ensemble is accepted with probability
-ensemble is accepted with probability
![$\displaystyle {\rm acc}[n \rightarrow m] = \min(1, {\rm e}^{ \beta ( {\mathbf c}_n - {\mathbf c}_m ) \cdot {\mathbf v}(x) + f_m - f_n}).$](img885.png) |
(6.15) |
In this approach, since the temperature is the same for all ensembles,
momentum rescaling (Eq. 6.14) must not be applied. We
will see in Section 6.3 how 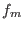 and
and 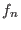 appearing into Eq. 6.15 are determined.
appearing into Eq. 6.15 are determined.
procacci
2021-12-29
![]() is therefore defined
by a coefficient
is therefore defined
by a coefficient
![]() (see Eq. 5.13) that
scales the potential energy
(see Eq. 5.13) that
scales the potential energy
![]() of the replica (the
vectorial form of the potential energy
of the replica (the
vectorial form of the potential energy ![]() is used because of
possible local scaling), i.e.,
is used because of
possible local scaling), i.e.,
![]() . In this sort of Hamiltonian tempering, the transition from
. In this sort of Hamiltonian tempering, the transition from
![]() to
to ![]() -ensemble is accepted with probability
-ensemble is accepted with probability