Next: Steered Molecular Dynamics Up: Metadynamics Simulation: history-dependent algorithms Previous: Metadynamics Simulation: history-dependent algorithms Contents Index
The second step is the metadynamics simulation itself, during which an history-dependent potential is constructed by summing, at regular time intervals, repulsive potential terms centered in the current position of the system in the space of the reaction coordinates. In its standard implementation, the history-dependent potential of metadynamics is given by a sum of small repulsive Gaussian, Eq.7.2. Some variants have been introduced, with the intent of improving the accuracy or the efficiency of the method[136,137]. In the ORAC program we have used Lucy's function[138] as a very efficient alternative to the use of Gaussian distributions.. It is defined as 7.1
The history dependent potential used during an ORAC simulation can therefore be written as
Using the standard metadynamics approach, during a simulation
the algorithm keeps on
adding terms to the history-dependent potential (the sum in
Eq.7.5) with the same constant rate
![]() . However, the
optimal solution would be to use a faster rate at the beginning of the
simulation, so as to produce a rough estimate of the free energy, and
then to reduce
. However, the
optimal solution would be to use a faster rate at the beginning of the
simulation, so as to produce a rough estimate of the free energy, and
then to reduce ![]() to refine this estimate[140]. This problem
corresponds to finding an optimal protocol for the evolution of the
modification factor in the original Wang-Landau algorithm. Various
solutions have been
proposed[141,133,142,143]
in which the energy
to refine this estimate[140]. This problem
corresponds to finding an optimal protocol for the evolution of the
modification factor in the original Wang-Landau algorithm. Various
solutions have been
proposed[141,133,142,143]
in which the energy
![]() in 7.3 is time-dependent.
We propose instead to add a term to the biasing potential with a given
probability
in 7.3 is time-dependent.
We propose instead to add a term to the biasing potential with a given
probability
![]() , depending parametrically on time.
For example, for
, depending parametrically on time.
For example, for
![]() , the evolution of the
rate would be given by
, the evolution of the
rate would be given by
![]() .
This procedure can be seen on average as an increasing
deposition interval
.
This procedure can be seen on average as an increasing
deposition interval ![]() , such that
, such that
![]() decreases in time.
In the present implementation of ORAC, three different choices are
available for the probability
decreases in time.
In the present implementation of ORAC, three different choices are
available for the probability
![]() : the default one is
simply
: the default one is
simply
![]() and corresponds to the standard metadynamics
algorithm. The second one is given by
and corresponds to the standard metadynamics
algorithm. The second one is given by
| (7.7) |
| (7.8) |
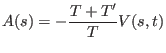 |
(7.9) |
The multiple walkers version of metadynamics algorithm[144]
was implemented in the parallel version of the code
through the MPI library.
This approach is based on running simultaneously
multiple replicas of the system, contributing equally
to the same history-dependent potential, and therefore
to the same free energy surface reconstruction.
For ![]() replicas,
replicas, ![]() can be written as a double sum
can be written as a double sum
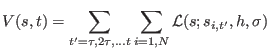 |
(7.10) |
In the ORAC distribution at http://www.chim.unifi.it/orac we provide some example of metadynamics simulations using Lucy's functions on multi-dimensional surfaces of simple molecules in the gas phase along with some ancillary codes for the analysis of the program output.
procacci 2021-12-29