The
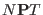 extended system is the most general among all
possible extended Lagrangians. All other ensemble can be in fact
obtained within the
same computational framework. We must stress [27] that the
computational overhead of the extended system formulation, due to the
introduction and handling of the extra degrees of freedom of the
barostat and thermostat variables, is rather modest and is negligible
with respect to a NVE simulation for large samples (
extended system is the most general among all
possible extended Lagrangians. All other ensemble can be in fact
obtained within the
same computational framework. We must stress [27] that the
computational overhead of the extended system formulation, due to the
introduction and handling of the extra degrees of freedom of the
barostat and thermostat variables, is rather modest and is negligible
with respect to a NVE simulation for large samples (
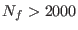 ) [26,25,27]. Therefore, a practical,
albeit inelegant way of switching among ensembles is simply to set the
inertia of the barostat and/or thermostat to a very large number. This
must be of course equivalent to decouple the barostat and/or the
thermostat from the true degrees of freedom. In fact, by setting
) [26,25,27]. Therefore, a practical,
albeit inelegant way of switching among ensembles is simply to set the
inertia of the barostat and/or thermostat to a very large number. This
must be of course equivalent to decouple the barostat and/or the
thermostat from the true degrees of freedom. In fact, by setting 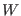 to
infinity3.11 in Eqs.
(3.23-3.27) we recover
the
to
infinity3.11 in Eqs.
(3.23-3.27) we recover
the 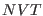 canonical ensemble equations of motion. Putting instead
canonical ensemble equations of motion. Putting instead 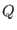 to infinity the
to infinity the 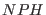 equations of motion are obtained. Finally, setting both
equations of motion are obtained. Finally, setting both
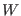 and
and 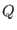 to infinity the
to infinity the 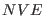 equations of motion are recovered.
equations of motion are recovered.
Switching to the 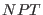 isotropic stress ensemble is less obvious.
One may define the kinetic term associated to barostat in the extended
Lagrangian as
isotropic stress ensemble is less obvious.
One may define the kinetic term associated to barostat in the extended
Lagrangian as
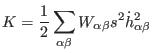 |
|
|
(3.78) |
such that a different inertia may in principle be assigned to each of
9 extra degrees of freedom of the barostat. Setting for example
one inhibits cell rotations [27].
This trick does not work,
unfortunately, to change to isotropic stress tensor.
In this case, there is only one independent
barostat degrees of freedom, namely the volume of the system.
In order to simulate isotropic cell fluctuations a set of five
constraints on the 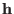 matrix are introduced which correspond to the
conditions:
matrix are introduced which correspond to the
conditions:
with
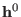 being some reference
being some reference 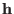 matrix.
These constraints are implemented naturally in the framework of
the multi time step velocity Verlet using the RATTLE algorithm
which evaluates iteratively the constraints force to satisfy
the constraints on both coordinates
matrix.
These constraints are implemented naturally in the framework of
the multi time step velocity Verlet using the RATTLE algorithm
which evaluates iteratively the constraints force to satisfy
the constraints on both coordinates 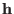 and velocities
and velocities
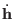 [27].
In Ref. [27] it is proved that the phase space sampled
by the
[27].
In Ref. [27] it is proved that the phase space sampled
by the
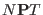 equations with the addition of the constraints
Eq. (3.83) correspond to that given by
equations with the addition of the constraints
Eq. (3.83) correspond to that given by 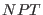 distribution function.
distribution function.
procacci
2021-12-29
![]() isotropic stress ensemble is less obvious.
One may define the kinetic term associated to barostat in the extended
Lagrangian as
isotropic stress ensemble is less obvious.
One may define the kinetic term associated to barostat in the extended
Lagrangian as
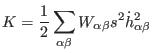
![]() matrix are introduced which correspond to the
conditions:
matrix are introduced which correspond to the
conditions: