Applications
As a first simple example we apply the double time integrator
(2.34) to the NVE simulation of flexible nitrogen at
100 K.
Table:
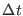 |
 |
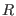 |
CPU |
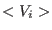 |
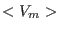 |
| 0.3 |
1 |
0.005 |
119 |
0.1912 |
-4.75 |
| 0.6 |
1 |
0.018 |
62 |
0.1937 |
-4.75 |
| 1.5 |
1 |
0.121 |
26 |
0.2142 |
-4.75 |
| 4.5 |
1 |
- |
- |
- |
- |
| 0.6 |
2 |
0.004 |
59 |
0.1912 |
-4.75 |
| 1.5 |
5 |
0.004 |
28 |
0.1912 |
-4.75 |
| 3.0 |
10 |
0.005 |
18 |
0.1912 |
-4.75 |
| 4.5 |
15 |
0.006 |
15 |
0.1912 |
-4.75 |
| 6.0 |
20 |
0.008 |
12 |
0.1912 |
-4.74 |
| 9.0 |
30 |
0.012 |
10 |
0.1911 |
-4.74 |
| 3.0 |
- |
0.001 |
14 |
- |
-4.74 |
| 6.0 |
- |
0.004 |
8 |
- |
-4.75 |
| 9.0 |
- |
0.008 |
6 |
- |
-4.74 |
The overall interaction potential is given by
Where 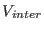 is the intermolecular potential described by a
Lennard-Jones model between all nitrogen atoms on different
molecules [80].
is the intermolecular potential described by a
Lennard-Jones model between all nitrogen atoms on different
molecules [80].
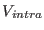 is instead the intramolecular stretching potential holding
together the two nitrogen atoms of each given molecule. We use here a simple
harmonic spring depending on the molecular bond length
is instead the intramolecular stretching potential holding
together the two nitrogen atoms of each given molecule. We use here a simple
harmonic spring depending on the molecular bond length 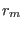 ,
namely:
,
namely:
with 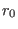 and
and 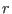 the equilibrium and instantaneous distance between
the nitrogen atoms, and
the equilibrium and instantaneous distance between
the nitrogen atoms, and 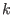 the force constant tuned to reproduce the
experimental gas-phase stretching frequency [81].
the force constant tuned to reproduce the
experimental gas-phase stretching frequency [81].
As a measure of the accuracy of the numerical integration we use the
adimensional energy conservation ratio [23,82,24,13]
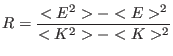 |
|
|
(2.44) |
where 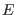 and
and 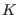 are the total and kinetic energy of the system,
respectively. In
table 1 we show the energy conservation ratio
are the total and kinetic energy of the system,
respectively. In
table 1 we show the energy conservation ratio 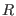 and CPU timings on a
IBM-43P/160MH/RS6000 obtained for flexible nitrogen at 100 K with the
r-RESPA integrator as a function of
and CPU timings on a
IBM-43P/160MH/RS6000 obtained for flexible nitrogen at 100 K with the
r-RESPA integrator as a function of  and
and
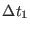 in
Eq. (2.34) and also for single time step
integrators. Results of integrators for rigid nitrogen using SHAKE are
also shown for comparison. The data in Table 1 refer to a 3.0
ps run without velocity rescaling. They were obtained starting all
runs from coordinates corresponding to the experimental
in
Eq. (2.34) and also for single time step
integrators. Results of integrators for rigid nitrogen using SHAKE are
also shown for comparison. The data in Table 1 refer to a 3.0
ps run without velocity rescaling. They were obtained starting all
runs from coordinates corresponding to the experimental 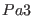 structure [83,84] of solid nitrogen and
from velocities taken randomly according to the Boltzmann distribution at
100 K.
structure [83,84] of solid nitrogen and
from velocities taken randomly according to the Boltzmann distribution at
100 K.
The entry in bold refers to the ``exact'' result,
obtained with a single time step integrator with a very small step size of
0.3 fs.
Note that 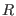 increases quadratically with the time step for single time step
integrators whereas r-RESPA is remarkably resistant to outer time step
size increase.
For example r-RESPA with
increases quadratically with the time step for single time step
integrators whereas r-RESPA is remarkably resistant to outer time step
size increase.
For example r-RESPA with
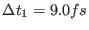 and
and 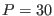 (i.e.
(i.e.
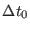 = 0.3 fs)
yields better accuracy on energy conservation
than single time step Velocity Verlet with
= 0.3 fs)
yields better accuracy on energy conservation
than single time step Velocity Verlet with
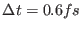 does, while
being more than six times faster.
Moreover, r-RESPA integrates all degrees of freedom of the systems and is
almost as efficient as Velocity Verlet with constraints on bonds.
It is also worth pointing out that energy averages for all r-RESPA
integrators is equal to the exact value,
while at single time step even a moderate step size increase results
in sensibly different
averages intra-molecular energies.
does, while
being more than six times faster.
Moreover, r-RESPA integrates all degrees of freedom of the systems and is
almost as efficient as Velocity Verlet with constraints on bonds.
It is also worth pointing out that energy averages for all r-RESPA
integrators is equal to the exact value,
while at single time step even a moderate step size increase results
in sensibly different
averages intra-molecular energies.
As a more complex example we now study a cluster of eight single
chain alkanes
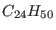 . In this case the potential contains
stretching, bending and torsional contributions plus the intermolecular
Van-der-Waals interactions between non bonded atoms. The parameter are
chosen according to the AMBER protocol [4] by assigning
the carbon and hydrogen atoms to the AMBER types ct and hc, respectively. For various dynamical and structural properties we
compare three integrators, namely a triple time step r-RESPA (R3) a
single time step integrator with bond constraints on
. In this case the potential contains
stretching, bending and torsional contributions plus the intermolecular
Van-der-Waals interactions between non bonded atoms. The parameter are
chosen according to the AMBER protocol [4] by assigning
the carbon and hydrogen atoms to the AMBER types ct and hc, respectively. For various dynamical and structural properties we
compare three integrators, namely a triple time step r-RESPA (R3) a
single time step integrator with bond constraints on 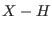 (S1) and a
single time step integrator with all bonds kept rigid (S). These three
integrators are tested, starting from the same phase space point,
against a single time step integrator (E) with a very small time step
generating the ``exact'' trajectory. In Fig. 2.1 we show
the time record of the torsional potential energy. The R3 integrator
generates a trajectory practically coincident with the ``exact''
trajectory for as long as 1.5 ps. The single time step with rigid
(S1) and a
single time step integrator with all bonds kept rigid (S). These three
integrators are tested, starting from the same phase space point,
against a single time step integrator (E) with a very small time step
generating the ``exact'' trajectory. In Fig. 2.1 we show
the time record of the torsional potential energy. The R3 integrator
generates a trajectory practically coincident with the ``exact''
trajectory for as long as 1.5 ps. The single time step with rigid
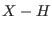 bonds also produces a fairly accurate trajectory, whereas the
trajectory generated by S quickly drifts away from the exact time
record. In Fig. 2.2 we show the power spectrum of the
velocity auto-correlation function obtained with R3, S1 and S. The
spectra are compared to the exact spectrum computed using the
trajectories generated by the accurate integrator E. We see that R3
and S1 generates the same spectral profile within statistical
error. In contrast, especially in the region above 800 wavenumbers, S
generates a spectrum which differs appreciably from the exact
one. This does not mean, of course, that S is unreliable for the
``relevant'' torsional degrees of freedom. Simply, we cannot a
priori exclude that keeping all bonds rigid will not have an impact
on the equilibrium structure of the alkanes molecules and on torsional
dynamics. Actually, in the present case, as long as torsional motions
are concerned all three integrators produce essentially identical
results. In 20 picoseconds of simulation, R3 S1 and S
predicted 60, 61, 60 torsional jumps, respectively, against the 59
jumps obtained with the exact integrator E. According to prescription of
Ref. [85], in order to avoid period doubling, we compute
the power spectrum of torsional motion form the auto-correlation
function of the vector product of two normalized vector perpendicular
to the dihedral planes. Rare events such as torsional jumps produce
large amplitudes long time scale oscillations in the time
auto-correlation function and therefore their contribution overwhelms
the spectrum which appears as a single broaden peak around
zero frequency. For this reason all torsions that did undergo a
barrier crossing were discarded in the computation of the power
spectrum. The power spectrum of the torsional motions is
identical for all integrators within statistical error when evaluated
over 20 ps of simulations.
bonds also produces a fairly accurate trajectory, whereas the
trajectory generated by S quickly drifts away from the exact time
record. In Fig. 2.2 we show the power spectrum of the
velocity auto-correlation function obtained with R3, S1 and S. The
spectra are compared to the exact spectrum computed using the
trajectories generated by the accurate integrator E. We see that R3
and S1 generates the same spectral profile within statistical
error. In contrast, especially in the region above 800 wavenumbers, S
generates a spectrum which differs appreciably from the exact
one. This does not mean, of course, that S is unreliable for the
``relevant'' torsional degrees of freedom. Simply, we cannot a
priori exclude that keeping all bonds rigid will not have an impact
on the equilibrium structure of the alkanes molecules and on torsional
dynamics. Actually, in the present case, as long as torsional motions
are concerned all three integrators produce essentially identical
results. In 20 picoseconds of simulation, R3 S1 and S
predicted 60, 61, 60 torsional jumps, respectively, against the 59
jumps obtained with the exact integrator E. According to prescription of
Ref. [85], in order to avoid period doubling, we compute
the power spectrum of torsional motion form the auto-correlation
function of the vector product of two normalized vector perpendicular
to the dihedral planes. Rare events such as torsional jumps produce
large amplitudes long time scale oscillations in the time
auto-correlation function and therefore their contribution overwhelms
the spectrum which appears as a single broaden peak around
zero frequency. For this reason all torsions that did undergo a
barrier crossing were discarded in the computation of the power
spectrum. The power spectrum of the torsional motions is
identical for all integrators within statistical error when evaluated
over 20 ps of simulations.
From these results it can be concluded that S1 and R3 are very likely
to produce essentially the same dynamics for all ``relevant'' degrees
of freedom. We are forced to state that also the integrator S appears
to accurately predict the structure and overall dynamics of the torsional degrees
of freedom at least for the 20 ps time span of this specific system.2.4 Since torsions are not
normal coordinates and couple to higher frequency internal coordinates
such as bending and stretching, the ability of the efficient S
integrator of correctly predicting low frequency dynamics and
structural properties cannot be assumed a priori and must
be, in principle, verified for each specific case. We also do not know
how the individual eigenvectors are affected by the integrators and,
although the overall density for S and S1 appears to be the same,
there might be considerable changes in the torsional dynamics. R3
does not require any assumption, is accurate everywhere in the
spectrum (see Fig. 2.2) and is as efficient as S. For
these reasons R3, or a multi-step version of the equally accurate S1,
must be the natural choice for the simulation of complex systems using
all-atoms models
procacci
2021-12-29
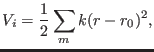
![]() increases quadratically with the time step for single time step
integrators whereas r-RESPA is remarkably resistant to outer time step
size increase.
For example r-RESPA with
increases quadratically with the time step for single time step
integrators whereas r-RESPA is remarkably resistant to outer time step
size increase.
For example r-RESPA with
![]() and
and ![]() (i.e.
(i.e.
![]() = 0.3 fs)
yields better accuracy on energy conservation
than single time step Velocity Verlet with
= 0.3 fs)
yields better accuracy on energy conservation
than single time step Velocity Verlet with
![]() does, while
being more than six times faster.
Moreover, r-RESPA integrates all degrees of freedom of the systems and is
almost as efficient as Velocity Verlet with constraints on bonds.
It is also worth pointing out that energy averages for all r-RESPA
integrators is equal to the exact value,
while at single time step even a moderate step size increase results
in sensibly different
averages intra-molecular energies.
does, while
being more than six times faster.
Moreover, r-RESPA integrates all degrees of freedom of the systems and is
almost as efficient as Velocity Verlet with constraints on bonds.
It is also worth pointing out that energy averages for all r-RESPA
integrators is equal to the exact value,
while at single time step even a moderate step size increase results
in sensibly different
averages intra-molecular energies.
![\includegraphics[scale=.60]{tors.eps}](img229.png)
![\includegraphics[scale=0.35]{vacf.eps}](img231.png)
![\includegraphics[scale=0.35]{vacf_tors.eps}](img232.png)