Tackling free energy estimates
The algorithm used to calculate the optimal weight factors, namely the
dimensionless free energy differences between ensembles (see
Sec. 6.2), is based on the Bennett acceptance
ratio[118,66] and on the free energy perturbation
formula[119]. We start by showing that the difference
between the dimensionless Hamiltonians appearing in the acceptance
ratio (see Eq. 6.8) can be viewed as the generalized
dimensionless work done on the system during the transition
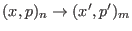 . The concept of generalized
dimensionless work in systems subject to mechanical and thermal
nonequilibrium changes has been extensively discussed in the
literature[116,127,117]. In particular it
has been shown (see Eq. 45 of Ref. [117]) that, in a
nonequilibrium realization performed with extended-Lagrangian
molecular dynamics[91], the generalized dimensionless work
is
. The concept of generalized
dimensionless work in systems subject to mechanical and thermal
nonequilibrium changes has been extensively discussed in the
literature[116,127,117]. In particular it
has been shown (see Eq. 45 of Ref. [117]) that, in a
nonequilibrium realization performed with extended-Lagrangian
molecular dynamics[91], the generalized dimensionless work
is
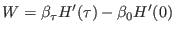 |
(6.18) |
where 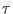 is the duration of the realization and
is the duration of the realization and
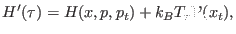 |
(6.19) |
where
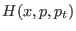 is defined in Eq. 6.13 and
is defined in Eq. 6.13 and
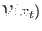 is a linear function of the configurational variables
is a linear function of the configurational variables 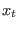 associated with the thermostat (see Eq. 42 of
Ref. [117]). For simplicity, in Eq. 6.19 we
have only reported the explicit time-dependence of the
temperature. Moreover, we have considered to deal with thermal changes
alone using constant-volume constant-temperature equations of
motion. Extending the treatment to constant-pressure
constant-temperature algorithms and to systems subject to generic
associated with the thermostat (see Eq. 42 of
Ref. [117]). For simplicity, in Eq. 6.19 we
have only reported the explicit time-dependence of the
temperature. Moreover, we have considered to deal with thermal changes
alone using constant-volume constant-temperature equations of
motion. Extending the treatment to constant-pressure
constant-temperature algorithms and to systems subject to generic
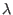 , e.g. mechanical, changes is
straightforward[117]. Note that, when no changes are
externally applied to the system,
, e.g. mechanical, changes is
straightforward[117]. Note that, when no changes are
externally applied to the system, 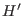 is exactly the quantity
conserved during an equilibrium constant-volume constant-temperature
simulation. Accordingly, the work
is exactly the quantity
conserved during an equilibrium constant-volume constant-temperature
simulation. Accordingly, the work 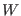 is zero. The above definition of
generalized dimensionless work is valid for arbitrary values of
is zero. The above definition of
generalized dimensionless work is valid for arbitrary values of
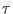 . In the special case of instantaneous thermal changes and
instantaneous variations of the microstate variables, as it occurs in
ST simulations, the times 0 and
. In the special case of instantaneous thermal changes and
instantaneous variations of the microstate variables, as it occurs in
ST simulations, the times 0 and 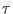 in
Eq. 6.18 refer to the states instantaneously
before and after the
in
Eq. 6.18 refer to the states instantaneously
before and after the
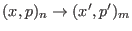 transition, respectively. Therefore, according to the notation
introduced above, Eq. 6.18 can be rewritten as
transition, respectively. Therefore, according to the notation
introduced above, Eq. 6.18 can be rewritten as
![$\displaystyle W[n \rightarrow m] = \beta_m H(x^\prime,p^\prime,p^\prime_t) - \beta_n H(x,p,p_t) + {\mathcal V}(x^\prime_t) - {\mathcal V}(x_t),$](img895.png) |
(6.20) |
where 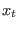 and
and
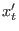 are the values of the configurational
thermostat-variables before and after the
are the values of the configurational
thermostat-variables before and after the
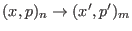 transition, respectively. In the first two
terms of the right-hand side of Eq. 6.20 we can
recognize the dimensionless Hamiltonians
transition, respectively. In the first two
terms of the right-hand side of Eq. 6.20 we can
recognize the dimensionless Hamiltonians
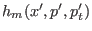 and
and
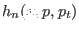 . It is
important to observe that, in generalized-ensemble simulations, an
arbitrary change of
. It is
important to observe that, in generalized-ensemble simulations, an
arbitrary change of 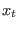 during a transition does not affect the
acceptance ratio nor the dynamics of the system. Therefore, by setting
during a transition does not affect the
acceptance ratio nor the dynamics of the system. Therefore, by setting
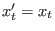 and generalizing to
and generalizing to 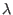 changes, we recover
the equality
changes, we recover
the equality
![$\displaystyle W[n \rightarrow m] = h_m(x^\prime,p^\prime,p^\prime_t) - h_n(x,p,p_t).$](img900.png) |
(6.21) |
Using
![$ W[n \rightarrow m]$](img901.png) , the acceptance ratio of
Eq. 6.8 becomes
, the acceptance ratio of
Eq. 6.8 becomes
![$\displaystyle \boxed{ {\rm acc}[n \rightarrow m] = \min(1, {\rm e}^{ \Delta f_{n \rightarrow m} - W[n \rightarrow m] }),}$](img902.png) |
(6.22) |
where
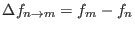 . The quantity
. The quantity
![$ W[n
\rightarrow m] - \Delta f_{n \rightarrow m}$](img904.png) can be interpreted as
the generalized dimensionless work dissipated in the transition (see
Eq. 17 of Ref. [117]).
can be interpreted as
the generalized dimensionless work dissipated in the transition (see
Eq. 17 of Ref. [117]).
Until now we have simply restated the acceptance ratio of SGE
simulations in terms of the generalized dimensionless work
![$ W[n \rightarrow m]$](img901.png) . The truly important aspect of this treatment is
that the knowledge of
. The truly important aspect of this treatment is
that the knowledge of
![$ W[n \rightarrow m]$](img901.png) and
and
![$ W[m \rightarrow n]$](img905.png) stored during the sampling gives us the possibility of evaluating the
optimal weights
stored during the sampling gives us the possibility of evaluating the
optimal weights
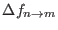 using the Bennett
method[118] reformulated with maximum likelihood
arguments[66,117]. For example, in ST simulations we
must take memory of the quantities
using the Bennett
method[118] reformulated with maximum likelihood
arguments[66,117]. For example, in ST simulations we
must take memory of the quantities
![$ W[n \rightarrow m] = (\beta_m -
\beta_n) V_n(x)$](img907.png) and
and
![$ W[m \rightarrow n] = (\beta_n - \beta_m)
V_m(x)$](img908.png) , where the subscripts of the potential energy indicate the
ensemble at which sampling occurs. The extension to Hamiltonian
tempering implemented in the ORAC program is straightforward
, where the subscripts of the potential energy indicate the
ensemble at which sampling occurs. The extension to Hamiltonian
tempering implemented in the ORAC program is straightforward
![$\displaystyle \boxed{W[n \rightarrow m] = \beta ({\mathbf c}_m - {\mathbf c}_n) \cdot {\mathbf v}_n(x)}$](img909.png) |
(6.23) |
with analogous expression for
![$ W[m \rightarrow n]$](img905.png) . In the case of SGE
simulations in the
. In the case of SGE
simulations in the 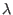 -space we have (substitute
Eq. 6.16 into Eq. 6.21 with
fixed coordinates and momenta)
-space we have (substitute
Eq. 6.16 into Eq. 6.21 with
fixed coordinates and momenta)
![$\displaystyle \boxed{ W[n \rightarrow m] = \beta k [ (r - \lambda_m)^2 - (r - \lambda_n)^2 ]. }$](img910.png) |
(6.24) |
Thus, for each pair of neighboring ensembles  and
and  , we generate
two collections of ``instantaneous generalized dimensionless works'':
, we generate
two collections of ``instantaneous generalized dimensionless works'':
![$ W_1[m \rightarrow n], W_2[m \rightarrow n], \dots,$](img911.png) etc. and
etc. and
![$ W_1[n
\rightarrow m], W_2[n \rightarrow m], \dots,$](img912.png) etc.. Let us denote
the number of elements of such collections with
etc.. Let us denote
the number of elements of such collections with
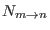 and
and
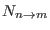 .
.
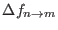 can be
calculated by solving the equation (see Eq. 27 of
Ref. [117])
can be
calculated by solving the equation (see Eq. 27 of
Ref. [117])
![$\displaystyle \boxed{ \sum_{i=1}^{N_{n \rightarrow m}} \left[ 1 + \frac{N_{n \r...
...\rm e}^{ W_j[m \rightarrow n] + \Delta f_{n \rightarrow m} } \right]^{-1} = 0,}$](img915.png) |
(6.25) |
that just corresponds to the Bennett acceptance ratio for
dimensionless quantities. It is important to point out that
Eq. 6.25 is valid for nonequilibrium transformations, does
not matter how far from equilibrium, and is rigorous only if the
initial microstates of the transformations are drawn from
equilibrium. Therefore care should be taken in verifying whether
convergence/equilibrium is reached in the adaptive procedure. It
should be noted that Eq. 6.25 is a straightforward
generalization of Eq. 8 of Ref. [66] that was specifically
derived for systems subject to mechanical changes.
Shirts et al.[66] proposed a way of evaluating the
square uncertainty (variance) of
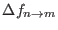 from
maximum likelihood methods, by also correcting the estimate in the
case of the restriction from fixed probability of forward and backward
work measurements to fixed number of forward and backward work
measurements. They provided a formula for systems subject only to
mechanical work. However, by following the arguments of
Ref. [117], it is straightforward to generalize the
variance:
from
maximum likelihood methods, by also correcting the estimate in the
case of the restriction from fixed probability of forward and backward
work measurements to fixed number of forward and backward work
measurements. They provided a formula for systems subject only to
mechanical work. However, by following the arguments of
Ref. [117], it is straightforward to generalize the
variance:
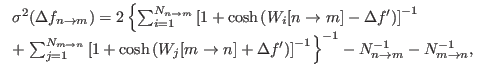 |
(6.26) |
where
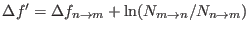 . The quantity
. The quantity
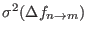 can be calculated once
can be calculated once
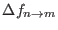 is recovered from Eq. 6.25.
is recovered from Eq. 6.25.
It is obvious that, in order to employ Eq. 6.25, both  and
and  ensembles must be visited at least one time. If statistics is
instead retrieved from one ensemble alone, say
ensembles must be visited at least one time. If statistics is
instead retrieved from one ensemble alone, say  , then we have to
resort to a different approach. The one we employ is consistent with
the previous treatment. In fact, in the limit that only one work
collection (specifically, the
, then we have to
resort to a different approach. The one we employ is consistent with
the previous treatment. In fact, in the limit that only one work
collection (specifically, the
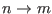 collection) is
available, Eq. 6.25 becomes[66] (compare with
Eq. 21 of Ref. [117])
collection) is
available, Eq. 6.25 becomes[66] (compare with
Eq. 21 of Ref. [117])
![$\displaystyle \boxed{ {\rm e}^{- \Delta f_{n \rightarrow m}} = N_{n \rightarrow m}^{-1} \sum_{i=1}^{N_{n \rightarrow m}} {\rm e}^{ - W_i[n \rightarrow m] },}$](img920.png) |
(6.27) |
thus recovering the well-known fact that the free energy is the
expectation value of the work exponential average[63].
procacci
2021-12-29
![]() . The concept of generalized
dimensionless work in systems subject to mechanical and thermal
nonequilibrium changes has been extensively discussed in the
literature[116,127,117]. In particular it
has been shown (see Eq. 45 of Ref. [117]) that, in a
nonequilibrium realization performed with extended-Lagrangian
molecular dynamics[91], the generalized dimensionless work
is
. The concept of generalized
dimensionless work in systems subject to mechanical and thermal
nonequilibrium changes has been extensively discussed in the
literature[116,127,117]. In particular it
has been shown (see Eq. 45 of Ref. [117]) that, in a
nonequilibrium realization performed with extended-Lagrangian
molecular dynamics[91], the generalized dimensionless work
is
![]() . The truly important aspect of this treatment is
that the knowledge of
. The truly important aspect of this treatment is
that the knowledge of
![]() and
and
![]() stored during the sampling gives us the possibility of evaluating the
optimal weights
stored during the sampling gives us the possibility of evaluating the
optimal weights
![]() using the Bennett
method[118] reformulated with maximum likelihood
arguments[66,117]. For example, in ST simulations we
must take memory of the quantities
using the Bennett
method[118] reformulated with maximum likelihood
arguments[66,117]. For example, in ST simulations we
must take memory of the quantities
![]() and
and
![]() , where the subscripts of the potential energy indicate the
ensemble at which sampling occurs. The extension to Hamiltonian
tempering implemented in the ORAC program is straightforward
, where the subscripts of the potential energy indicate the
ensemble at which sampling occurs. The extension to Hamiltonian
tempering implemented in the ORAC program is straightforward
![]() from
maximum likelihood methods, by also correcting the estimate in the
case of the restriction from fixed probability of forward and backward
work measurements to fixed number of forward and backward work
measurements. They provided a formula for systems subject only to
mechanical work. However, by following the arguments of
Ref. [117], it is straightforward to generalize the
variance:
from
maximum likelihood methods, by also correcting the estimate in the
case of the restriction from fixed probability of forward and backward
work measurements to fixed number of forward and backward work
measurements. They provided a formula for systems subject only to
mechanical work. However, by following the arguments of
Ref. [117], it is straightforward to generalize the
variance:
![]() and
and ![]() ensembles must be visited at least one time. If statistics is
instead retrieved from one ensemble alone, say
ensembles must be visited at least one time. If statistics is
instead retrieved from one ensemble alone, say ![]() , then we have to
resort to a different approach. The one we employ is consistent with
the previous treatment. In fact, in the limit that only one work
collection (specifically, the
, then we have to
resort to a different approach. The one we employ is consistent with
the previous treatment. In fact, in the limit that only one work
collection (specifically, the
![]() collection) is
available, Eq. 6.25 becomes[66] (compare with
Eq. 21 of Ref. [117])
collection) is
available, Eq. 6.25 becomes[66] (compare with
Eq. 21 of Ref. [117])