- NAME
ERFC_SPLINE - Use spline to compute the complementary error
function used for electrostatics in direct space
- SYNOPSIS
ERFC_SPLINE erfc_bin
ERFC_SPLINE erfc_bin corrected rcut
- DESCRIPTION
By default ORAC uses a 5 parameter expansion to compute the
complementary error function required by the direct space
electrostatic potential (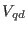 in Eq. 4.20). With the command
ERFC_SPLINE this expansion is replaced by a B-spline.
The function
in Eq. 4.20). With the command
ERFC_SPLINE this expansion is replaced by a B-spline.
The function
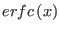 is splined from
is splined from 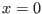 to
to
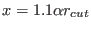 , where
, where 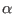 and
and 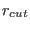 are the Ewald sum parameter and
the radial cutoff, respectively. The argument erfc_bin is
the bin size of the spline. The usage of the ERFC_SPLINE option
is useful when running on workstations where a saving of 10-15 % in
CPU time is usually obtained. ERFC_SPLINE may also be used
to speed up the Ewald method. By specifying the directive corrected ORAC corrects for the reciprocal lattice cutoff for all
intermolecular interactions in the
direct lattice using the same oscillating potential of Eq. (4.47)
(see Sec. 4.4) used for correcting the intra-molecular
potential (see ERF_CORR in this environment. This allows
the use shorter cutoffs in reciprocal space (or coarser grids in SPME).
The argument rcut corresponds to the maximum distance for the spline table.
Must be larger than the current cutoff (see examples).
are the Ewald sum parameter and
the radial cutoff, respectively. The argument erfc_bin is
the bin size of the spline. The usage of the ERFC_SPLINE option
is useful when running on workstations where a saving of 10-15 % in
CPU time is usually obtained. ERFC_SPLINE may also be used
to speed up the Ewald method. By specifying the directive corrected ORAC corrects for the reciprocal lattice cutoff for all
intermolecular interactions in the
direct lattice using the same oscillating potential of Eq. (4.47)
(see Sec. 4.4) used for correcting the intra-molecular
potential (see ERF_CORR in this environment. This allows
the use shorter cutoffs in reciprocal space (or coarser grids in SPME).
The argument rcut corresponds to the maximum distance for the spline table.
Must be larger than the current cutoff (see examples).
- EXAMPLES
ERFC_SPLINE 0.01
A B-spline is used to evaluate the direct space sum. To evaluate the
B-spline the original function is computed on a grid of 0.01 bin
size.
ERFC_SPLINE 0.01 corrected 14.0
The splined potential is now given by standard the direct lattice
Ewald term plus the
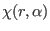 potential defined in Eq.
(see also command ERF_CORR in this environment). The B-spline
look up table is done for distances
potential defined in Eq.
(see also command ERF_CORR in this environment). The B-spline
look up table is done for distances
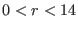 .
.
- WARNINGS
rcut is an atomic cutoff.
Always define rcut large enough to assure that all atoms
are included within rcut for any molecular pair.
E. g., if 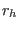 the largest cutoff defined in the structured command
MTS_RESPA (&INTEGRATOR) and the molecule has a
maximum extension in any possible direction of
the largest cutoff defined in the structured command
MTS_RESPA (&INTEGRATOR) and the molecule has a
maximum extension in any possible direction of 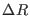 , choose
, choose

procacci
2021-12-29
![]()