- NAME
SETUP - This is the basic command to decide which kind of
simulation, Hamiltonian SGE simulation or SGE simulation in
the space of collective coordinates, one wants to carry out. This
command also defines the number of ensembles, the scaling options and
the restart option.
- SYNOPSIS
SETUP 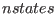 [
[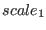
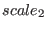
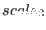 ]
] 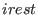
- DESCRIPTION
Hamiltonian SGE simulations.
If the parameters
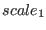 ,
, 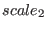 and
and 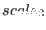 (real numbers) are specified in the
SETUP command, then a Hamiltonian SGE simulation with total or
partial scaling of the potential energy is performed
(simulated-tempering and solute-tempering like simulations,
respectively). In such a case the SETUP command is used to
define the number of ensembles (nstates; integer number) and the
lowest scaling factor (i.e the highest temperature) of the last
ensemble. The number of replicas in the SGE simulations is equal to
the number of processors passed to the MPI routines (
(real numbers) are specified in the
SETUP command, then a Hamiltonian SGE simulation with total or
partial scaling of the potential energy is performed
(simulated-tempering and solute-tempering like simulations,
respectively). In such a case the SETUP command is used to
define the number of ensembles (nstates; integer number) and the
lowest scaling factor (i.e the highest temperature) of the last
ensemble. The number of replicas in the SGE simulations is equal to
the number of processors passed to the MPI routines (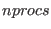 ). At
variance with REM,
). At
variance with REM, 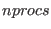 may be not equal to
may be not equal to 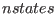 . The restart
option of a SGE simulation is controlled by irest (integer
number). The three parameters,
. The restart
option of a SGE simulation is controlled by irest (integer
number). The three parameters, 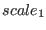 ,
, 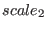 and
and 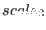 , can
be different and refer to scaling features of different parts of the
potential energy.
, can
be different and refer to scaling features of different parts of the
potential energy. 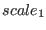 refers to the bending, stretching and
improper torsional potentials,
refers to the bending, stretching and
improper torsional potentials, 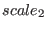 to the (proper) torsional
potential and to the 1-4 non-bonded interactions and
to the (proper) torsional
potential and to the 1-4 non-bonded interactions and 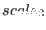 refers
to the non bonded potential. IMPORTANT NOTE: when the
Ewald summation is used together with the command SEGMENT(&SGE),
refers
to the non bonded potential. IMPORTANT NOTE: when the
Ewald summation is used together with the command SEGMENT(&SGE), 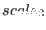 scales only the direct (short-ranged)
part of the electrostatic interactions and the (long-ranged)
reciprocal part has a scaling factor of 1 (i.e. these interactions are
not scaled). If
scales only the direct (short-ranged)
part of the electrostatic interactions and the (long-ranged)
reciprocal part has a scaling factor of 1 (i.e. these interactions are
not scaled). If
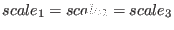 , then an equal scaling
is applied to all parts of the potential (it corresponds to a
simulated tempering simulation). If
, then an equal scaling
is applied to all parts of the potential (it corresponds to a
simulated tempering simulation). If 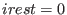 , the run is restarted
from a previous one. This implies that the directories PARXXXX are
present and are equal in number to
, the run is restarted
from a previous one. This implies that the directories PARXXXX are
present and are equal in number to 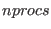 , i.e. the number of
replicas. If
, i.e. the number of
replicas. If
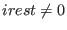 then the run refers to a cold start from
scratch and
SGE simulations in the space of collective
coordinates.
then the run refers to a cold start from
scratch and
SGE simulations in the space of collective
coordinates.
If the parameters 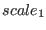 ,
, 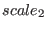 and
and 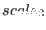 are not specified in the SETUP command, then a SGE simulation in
the space of collective coordinates is performed. In such a case the
SETUP command is used to define the number of ensembles
(
are not specified in the SETUP command, then a SGE simulation in
the space of collective coordinates is performed. In such a case the
SETUP command is used to define the number of ensembles
(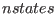 ) and the restart option (
) and the restart option (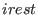 ). Their meaning has been
explained above. The collective coordinates are defined using the ADD_STR_BONDS (bond coordinates), ADD_STR_BENDS (bending
coordinates) and ADD_STR_TORS (torsional coordinates). These
commands are defined in the &POTENTIAL environment and must be used
in the following form
). Their meaning has been
explained above. The collective coordinates are defined using the ADD_STR_BONDS (bond coordinates), ADD_STR_BENDS (bending
coordinates) and ADD_STR_TORS (torsional coordinates). These
commands are defined in the &POTENTIAL environment and must be used
in the following form
ADD_STR_BONDS 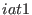
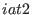
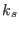
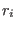
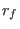
ADD_STR_BENDS 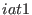
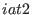
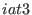
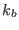
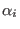
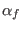
ADD_STR_TORS 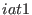
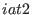
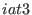
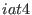
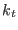
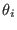
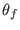
These expressions define the
additional harmonic potential entering into
Eq. 6.24. For example, if we perform a SGE simulation
in the space of a distance between two atoms, then ADD_STR_BONDS must be used. The parameters 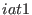 and
and 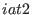 are
the atom numbers,
are
the atom numbers, 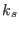 corresponds to
corresponds to 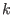 of Eq. 6.24
and
of Eq. 6.24
and 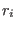 and
and 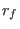 define the intermediate ensembles as follows:
define the intermediate ensembles as follows:
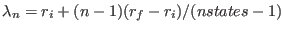 , where
, where
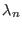 is the parameter characteristic of the ensemble
is the parameter characteristic of the ensemble  with
with
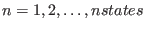 (see Eq. 6.24).
(see Eq. 6.24).
- EXAMPLES
SETUP 5 1. 1. 0.6 1
A Hamiltonian SGE simulation is
performed. The non bonded potential (direct part) is scaled using a
geometric progression, while the other potential terms are
unscaled. The number of ensembles is 5.
SETUP 4 1
ADD_STR_BONDS 22 143 1. 10. 14.5
ADD_STR_BENDS 25 33 67 2. 100. 130.
A SGE simulation in the space of collective coordinates is performed
using 4 ensembles. The collective coordinates are one bond and one
bending. The bond is related to the atoms 22 and 143. The bending is
defined by the atoms 25, 33 and 67. The ensembles are defined by 2
parameters,
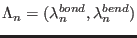 , where
the bond related parameters are
, where
the bond related parameters are
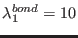 ,
,
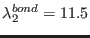 ,
,
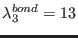 ,
,
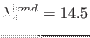 (in Å) and the bending related parameters is
(in Å) and the bending related parameters is
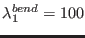 ,
,
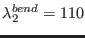 ,
,
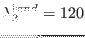 ,
,
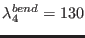 (in degrees). Therefore the
transition of a replica from the ensemble
(in degrees). Therefore the
transition of a replica from the ensemble 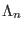 to the ensemble
to the ensemble
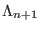 involves a synchronous change of both parameters,
i.e.
involves a synchronous change of both parameters,
i.e.
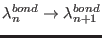 and
and
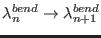 . Finally, the
harmonic force constants (see Eq. 6.24) are 1 and 2
kcal mol
. Finally, the
harmonic force constants (see Eq. 6.24) are 1 and 2
kcal mol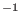 for bond and bending, respectively.
for bond and bending, respectively.

procacci
2021-12-29
![]()