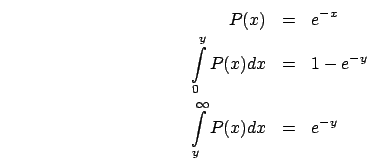Lezione n.3 - 13/3/2007
- Lo stato del sistema (microstato) è rappresentato da un punto nello
spazio delle fasi
In meccanica quantistica lo spazio delle fasi è lo spazio dei numeri
quantici del sistema
Quando il sistema passa da uno stato  ad uno stato
ad uno stato  il punto
si sposta:
il punto
si sposta:
L'evoluzione del sistema è descritta da una traiettoria nello
spazio delle fasi.
Se sono fissate delle condizioni macroscopiche (es. E,V=fissi) il
sistema percorre solo una ``superficie'' dello spazio delle fasi
- Insieme statistico o ensemble:
insieme di tutti i microstati compatibili con un dato stato macroscopico.
La media di una grandezza osservabile  è la media statistica (o
di ensemble) dei valori di
è la media statistica (o
di ensemble) dei valori di 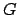 corrispondenti a un certo microstato
corrispondenti a un certo microstato
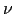 :
:
In pratica, se siamo in grado di stimare una funzione di distribuzione
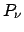 e di calcolare il corrispondente
e di calcolare il corrispondente 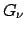 , possiamo calcolare
, possiamo calcolare
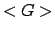 .
.
Il punto di partenza per un'interpretazione microscopica della termodinamica
è un principio fondamentale che riguarda la distribuzione dei microstati.
Per illustrarlo, partiamo dal sistema concettualmente più semplice:
un sistema di cui sono noti e determinati l'energia totale 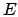 e
le ``dimensioni'', queste ultime tipicamente specificate come
numero di particelle
e
le ``dimensioni'', queste ultime tipicamente specificate come
numero di particelle 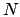 e volume totale
e volume totale 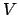 .
.
Nella termodinamica si studiano le relazioni tra queste poche grandezze
che caratterizzano il sistema. Il sistema è un punto nello spazio
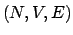 1:
1:
Figura:
sistema N,V,E
![\includegraphics[%
width=0.5\textwidth]{pianoEV.eps}](img15.png) |
Le relazioni si studiano con l'introduzione di una funzione dipendente
da 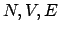 , che svolge il ruolo di ``potenziale'', cioè indica
la direzione delle trasformazioni spontanee. Questa funzione è l'entropia:
, che svolge il ruolo di ``potenziale'', cioè indica
la direzione delle trasformazioni spontanee. Questa funzione è l'entropia:
Nella visione microscopica, ad ogni punto 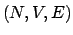 corrisponde un
insieme statistico, che si chiama insieme microcanonico.
corrisponde un
insieme statistico, che si chiama insieme microcanonico.
L'assunzione da cui si parte è il seguente principio di equiprobabilità
a priori:
In un sistema isolato con una data energia totale 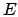 e un
dato volume
e un
dato volume 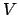 e numero di particelle
e numero di particelle 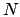 , all'equilibrio, tutti
i microstati sono ugualmente probabili.
, all'equilibrio, tutti
i microstati sono ugualmente probabili.
Quest'ipotesi è puramente ragionevole; non c'è nessun motivo di pensare
il contrario2. Notiamo che una semplice assunzione di questo tipo non vale
se:
- Il sistema non è isolato, cioè può scambiare energia o particelle
con l'esterno, in modo tale che
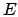 e/o
e/o 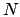 variano; infatti in
questo caso l'esterno può influenzare la probabilità di certi stati
variano; infatti in
questo caso l'esterno può influenzare la probabilità di certi stati
- il sistema è fuori dell'equilibrio (si può ``forzare'', o ``vincolare'',
il sistema in modo che alcuni microstati siano meno probabili, o addirittura
impossibili; ad es. vincolando metà delle molecole a stare nella metà
di destra del contenitore)
Per esprimere in termini quantitativi l'assunzione appena enunciata
definiamo innanzitutto 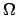 come il numero totale dei microstati.
È abbastanza intuitivo che
come il numero totale dei microstati.
È abbastanza intuitivo che 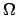 dipende sia dall'energia del
sistema, sia dalle sue dimensioni:
dipende sia dall'energia del
sistema, sia dalle sue dimensioni:
Il principio di equiprobabilità a priori si può quindi scrivere in
termini della funzione di distribuzione 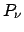 :
:
per ogni microstato 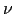 , cioè
, cioè 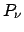 è costante su tutto l'ensemble.
è costante su tutto l'ensemble.
Notiamo che 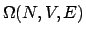 è a rigore un numero, però possiamo trattarla
come una funzione continua delle sue variabili, analogamente
a quanto si fa per la distribuzione spaziale del numero di particelle
di un sistema3.
è a rigore un numero, però possiamo trattarla
come una funzione continua delle sue variabili, analogamente
a quanto si fa per la distribuzione spaziale del numero di particelle
di un sistema3.
In questo caso possiamo definire l'entropia come
 |
(1) |
dove 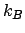 , la costante di Boltzmann, si ricava dal confronto con
le misure sperimentali.
, la costante di Boltzmann, si ricava dal confronto con
le misure sperimentali. 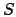 definita in questo modo -al di là del
valore numerico esatto- possiede le proprietà fondamentali dell'entropia
termodinamica:
definita in questo modo -al di là del
valore numerico esatto- possiede le proprietà fondamentali dell'entropia
termodinamica:
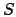 è estensiva; infatti se si immagina il sistema come
composto di due sottosistemi
è estensiva; infatti se si immagina il sistema come
composto di due sottosistemi 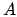 e
e 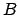 (ad esempio, uno di
(ad esempio, uno di 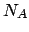 e uno di
e uno di 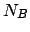 particelle, con
particelle, con 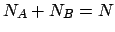 )4, allora
)4, allora
Esempio: quattro particelle 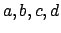 in due ``livelli'': ciascuna
delle due metà del contenitore. Poiché ogni particella può stare in
entrambi i livelli, il sistema ha in due ``livelli'': ciascuna
delle due metà del contenitore. Poiché ogni particella può stare in
entrambi i livelli, il sistema ha
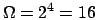 microstati. Ora
consideriamo (mentalmente) i due sottosistemi microstati. Ora
consideriamo (mentalmente) i due sottosistemi 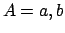 e e 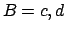 .
I microstati di ciascun sottosistema sono .
I microstati di ciascun sottosistema sono
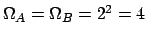 : :
Gli stati totali sono la combinazione di ciascun microstato del sistema
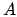 con ciascun microstato di con ciascun microstato di 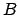 , cioè , cioè
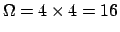 stati: stati:
|
- L'entropia è massima all'equilibrio. Per forzare il sistema
in una condizione di non-equilibrio (ma sempre con gli stessi valori
di
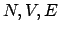 ) devo introdurre un vincolo aggiuntivo. Ad esempio, posso
(pensare di) portare il sistema fuori dall'equilibrio separando
le
) devo introdurre un vincolo aggiuntivo. Ad esempio, posso
(pensare di) portare il sistema fuori dall'equilibrio separando
le 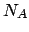 molecole dalle
molecole dalle 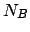 , ciascuna in una porzione
di volume, tale che
, ciascuna in una porzione
di volume, tale che 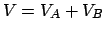 ; quando rimuovo il vincolo lasciando
che il sistema si evolva liberamente, esso si porta nuovamente nella
condizione di equilibrio, cioè con tutte le molecole che occupano
tutto il volume. Dunque l'entropia del sistema+vincolo deve essere
minore di quella del sistema originario. Infatti, ciascuno
dei due sottoinsiemi di molecole non ha a disposizione tutti gli stati
che ha a disposizione in assenza di vincolo.
; quando rimuovo il vincolo lasciando
che il sistema si evolva liberamente, esso si porta nuovamente nella
condizione di equilibrio, cioè con tutte le molecole che occupano
tutto il volume. Dunque l'entropia del sistema+vincolo deve essere
minore di quella del sistema originario. Infatti, ciascuno
dei due sottoinsiemi di molecole non ha a disposizione tutti gli stati
che ha a disposizione in assenza di vincolo.
Nell'esempio appena citato, se imponiamo che due particelle siano
in un livello e due nell'altro, si ha solo un microstato:
e 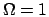 |
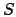 è una funzione monotona crescente di
è una funzione monotona crescente di 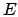 . Infatti dalla
termodinamica sappiamo che
. Infatti dalla
termodinamica sappiamo che
Secondo la definizione data (![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) ), questa diseguaglianza
diventa
), questa diseguaglianza
diventa
o
(per definizione 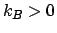 ). Perché la disuguaglianza valga, bisogna
che
). Perché la disuguaglianza valga, bisogna
che 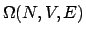 sia una funzione crescente di
sia una funzione crescente di 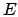 per
per 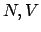 fissi. Il che è ragionevole: se l'energia totale aumenta, aumentano
anche i modi di distribuirla tra le particelle.
fissi. Il che è ragionevole: se l'energia totale aumenta, aumentano
anche i modi di distribuirla tra le particelle.
Consideriamo adesso un sistema, non più isolato, ma che può scambiare
energia con l'ambiente esterno, in particolare con un bagno termico
che ne mantiene la temperatura al valore 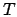 .
.
Un tale sistema è rappresentato, in termodinamica, da un punto nello
spazio 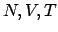 . Ad ogni punto di questo spazio corrisponde un insieme
statistico che in questo caso si chiama insieme canonico.
. Ad ogni punto di questo spazio corrisponde un insieme
statistico che in questo caso si chiama insieme canonico.
Figura:
(da Chandler): Stati di un sistema chiuso in un bagno termico
![\includegraphics[%
width=1\textwidth,
keepaspectratio]{chand-3-2.ps}](img48.png) |
Da un punto di vista microscopico la situazione appare più complessa
che nel caso precedente. I microstati compatibili con le condizioni
date sono tutti quelli corrispondenti ad una certa energia totale
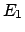 (come nel microcanonico), ma anche tutti quelli corrispondenti
ad
(come nel microcanonico), ma anche tutti quelli corrispondenti
ad 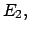 etc. Mi posso domandare qual è il peso relativo delle
varie classi di stati (
etc. Mi posso domandare qual è il peso relativo delle
varie classi di stati (
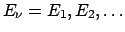 ).
).
Per rispondere facciamo riferimento a quello che sappiamo sull'insieme
microcanonico. Dobbiamo però aggiungere l'ipotesi che la coppia
 sia isolata, cioè che
sia isolata, cioè che
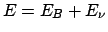 sia fisso (
sia fisso (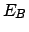 = energia
del bagno termico). Posso sempre soddisfare quest'ipotesi, scegliendo
il bagno opportunamente.
= energia
del bagno termico). Posso sempre soddisfare quest'ipotesi, scegliendo
il bagno opportunamente.
La coppia
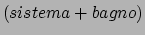 è un sistema
è un sistema 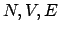 a cui corrisponde
un insieme microcanonico:
a cui corrisponde
un insieme microcanonico:
Figura:
(da Chandler): Insieme canonico come sottosistema di un insieme microcanonico
![\includegraphics[%
width=1\textwidth]{chand-3-3.ps}](img55.png) |
Sappiamo che gli stati di questo ``super-sistema'' sono equiprobabili.
Ma la domanda che ci siamo posti è: qual è la probabilità di osservare
uno qualsiasi tra i microstati in cui l'energia del sistema
osservato è 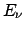 ?
?
Chiaramente
cioè, questa probabilità è proporzionale al numero degli stati del
super-sistema in cui il sistema osservato ha energia 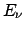
Ora il passaggio chiave è il seguente: questo numero è uguale al numero
degli stati in cui il bagno ha energia 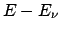 :
:
(notare che è qui che sfruttiamo l'ipotesi che il super-sistema sia
isolato).
È un problema combinatorio: se noi consideriamo tutti i possibili
modi di disporre  oggetti in un certo spazio, il numero di modi
in cui
oggetti in un certo spazio, il numero di modi
in cui  di questi oggetti si trovano in una determinata regione
è uguale al numero di modi in cui
di questi oggetti si trovano in una determinata regione
è uguale al numero di modi in cui 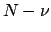 si trovano nel resto dello
spazio.
si trovano nel resto dello
spazio.
Ora facciamo due ulteriori assunzioni che derivano dalle grandi dimensioni
del bagno:
- L'energia del bagno è enormemente maggiore di quella del sistema:
- I livelli di energia del super-sistema sono così vicini da formare
un continuo, in modo tale che la funzione
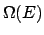 e continua
e
e continua
e
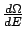 è definita.
è definita.
In questo caso posso espandere
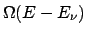 in serie di Taylor.
Lo stesso posso fare per il suo logaritmo -ricordiamo che la quantità
che ha maggiore significato fisico non è
in serie di Taylor.
Lo stesso posso fare per il suo logaritmo -ricordiamo che la quantità
che ha maggiore significato fisico non è 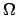 , ma
, ma 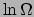 5:
5:
ed usando la definizione di 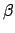
valida nel limite
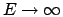 .
.
Quindi in questo limite
o
Normalizzando le probabilità
si ha:
Questa derivazione della funzione di distribuzione canonica è può
apparire un po' astratta e artificiosa. Quali sono i suoi limiti?
La validità di questa trattazione dipende dall'esistenza e dal significato
delle grandezze che usiamo, cioè essenzialmente di
Se questa fosse una funzione indefinibile, immisurabile, discontinua
o mostruosamente oscillante, l'equazione precedente sarebbe formalmente
corretta ma poco utile; il fatto che
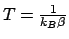 sia
una grandezza fisica ben definita le dà invece un significato.
sia
una grandezza fisica ben definita le dà invece un significato.
È lecito quindi aspettarsi che una trattazione simile si possa applicare
a tutti i problemi riconducibili allo stesso modello: un sistema in
equilibrio con una ``riserva'', il tutto isolato, e tale che si
può definire una funzione 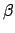 , ovvero una funzione
, ovvero una funzione 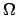 a logaritmo derivabile.
a logaritmo derivabile.
Prendiamo una scacchiera di 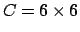 caselle e disponiamoci a
caso, con l'aiuto di due dadi,
caselle e disponiamoci a
caso, con l'aiuto di due dadi, 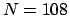 pedine. Un risultato può essere
quello della figura
pedine. Un risultato può essere
quello della figura ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) :
:
Figura:
La scacchiera all'inizio del gioco con il numero di pedine in ciascuna
casella
![\includegraphics[%
clip,
scale=0.9,
angle=181]{Sel-1.eps}](img80.png) |
Da un punto di vista statistico possiamo descrivere la situazione
contando le caselle che contengono 1 pedina, quelle che ne contengono
2, etc., e rappresentiamo il risultato in un istogramma (figura cap:Selinger-A8.2).
Come si vede, non tutte le caselle contengono 3 pedine (la media),
anzi ci sono più caselle con 1,2, o 4 pedine.
Figura:
Numero di caselle con 0,1,2, etc. pedine (108 pedine su 36 caselle).
![\includegraphics[%
width=0.4\paperwidth,
keepaspectratio,
angle=2]{Sel-2.eps}](img81.png) |
Ora muoviamo a caso le pedine tra le caselle. Per fare questo tiriamo
i dadi due volte per ogni mossa: il primo tiro indica la casella da
cui levare una pedina (se la casella è vuota, si ritira); il secondo
tiro, dove metterla. Ripetiamo la cosa molte volte per simulare un
rimescolamento efficiente. Notiamo che 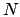 si conserva. Dopo 1000
mosse, ad esempio, la situazione è quella della figura cap:Selinger-A8.3.
Vediamo che la distribuzione si è modificata (ora ci sono anche molte
caselle vuote).
si conserva. Dopo 1000
mosse, ad esempio, la situazione è quella della figura cap:Selinger-A8.3.
Vediamo che la distribuzione si è modificata (ora ci sono anche molte
caselle vuote).
Figura:
Distribuzione dopo 1000 mosse.
![\includegraphics[%
width=0.4\paperwidth,
keepaspectratio,
angle=2]{Sel-3.eps}](img82.png) |
Se andiamo avanti con rimescolamenti di 1000 mosse otterremo istogrammi
(distribuzioni) diversi. Se volessimo fare una statistica potremmo
fare una media sui vari istogrammi che otteniamo. Come vi aspettate
che sia l'istogramma mediato su 500 rimescolamenti?
La risposta è riportata nell'ultima figura (cap:Selinger-A8.4).
Vediamo che in media ci sono molte caselle vuote, un po' meno caselle
con 1 pedina, ancora meno con 2, e sempre a scendere fino a medie
molto basse per numeri di occupazione alti, tipo 13 o maggiore.
Figura:
Distribuzione mediata su 500 mescolamenti ciascuno di 1000 mosse.
![\includegraphics[%
width=0.4\paperwidth,
keepaspectratio,
angle=90]{Sel-4.eps}](img83.png) |
Non stupirà scoprire che la frequenza relativa di caselle con 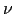 pedine è circa
pedine è circa
equazione che diventa sempre più precisa quanto più alto è 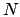 ; in
sostanza, abbiamo ottenuto una distribuzione canonica.
; in
sostanza, abbiamo ottenuto una distribuzione canonica.
Ed infatti questo semplice esempio può essere trattato in modo perfettamente
analogo a come abbiamo affrontato gli insiemi statistici, se al numero
di pedine facciamo corrispondere l'energia.
Ogni casella rappresenta una copia del sistema nell'insieme canonico.
Il resto delle caselle svolge il ruolo del bagno termico. La scacchiera,
come il ``super-sistema'' microcanonico in cui è immerso un sistema
canonico, è isolata e, assumendo che tutte le configurazioni sono
ugualmente accessibili, all'equilibrio.
La quantità 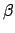 può essere sia calcolata analiticamente6 che misurata con una semplice simulazione, e rappresenta a tutti
gli effetti la ``temperatura reciproca'' del sistema.
può essere sia calcolata analiticamente6 che misurata con una semplice simulazione, e rappresenta a tutti
gli effetti la ``temperatura reciproca'' del sistema.
Nell'insieme microcanonico abbiamo stabilito un collegamento tra la
grandezza statistica rilevante (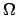 ) e una quantità termodinamica,
) e una quantità termodinamica,
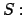
Esiste un analogo collegamento tra la grandezza statistica rilevante
nell'insieme canonico (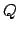 ) e l'energia libera di Helmholtz,
) e l'energia libera di Helmholtz, 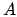 ,
per la quale valgono le relazioni
,
per la quale valgono le relazioni
se usiamo la seguente definizione di 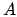 :
:
Proviamo ad esempio a calcolare l'energia interna del sistema. Nell'insieme
canonico questa è data dalla media dell'energia
Con la definizione di 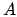 sopra riportata si ha:
sopra riportata si ha:
che è esattamente quello che si ottiene in termodinamica dalle relazioni
(![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) ) e (
) e (![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) )
)
- Dal calcolo combinatorio si ha
(numero di modi di disporre 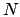 oggetti indistinguibili in
oggetti indistinguibili in 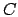 celle)
celle)
- numero medio di pedine per cella:
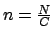
- calcolo di
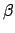 per alti valori di
per alti valori di 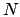 . Si ha:
. Si ha:
Inoltre, se 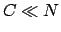
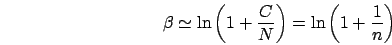 |
(4) |
Notare che nel limite 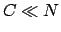 , cioè
, cioè
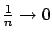 ,
si può applicare
,
si può applicare
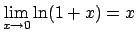 , e quindi
, e quindi
 |
(5) |
- calcolo di
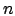 come media d'insieme:
come media d'insieme:
Gli integrali valgono:
e in conclusione
che è in accordo con eq:scacc-beta-nu, valida negli stessi
limiti
- funzione di distribuzione:
cioè, la legge di distribuzione dipende dal numero d'occupazione scalato
(rispetto alla media),
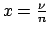 . Alcune interessanti relazioni:
. Alcune interessanti relazioni:
da queste discende ad esempio che
- la frazione di caselle con occupazione inferiore alla media (
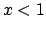 )
è
)
è
- la mediana di
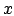 , cioè il valore che lascia uguale popolazione al
disopra e al disotto, è
, cioè il valore che lascia uguale popolazione al
disopra e al disotto, è
- ...1
- un vero spazio, a tre dimensioni!
- ... contrario2
- si può intuire una sua connessione con il teorema di Liouville
- ... sistema3
- per una discussione di questo punto cfr. Chandler, p. 58.
- ...4
- notare che il volume di entrambi i sottosistemi resta quello totale;
una situazione diversa è se il sistema viene realmente
diviso in due parti, con l'introduzione di un vincolo, cfr. il punto
successivo
- ...5
- ad esempio,
 è definita a meno di un fattore, mentre
è definita a meno di un fattore, mentre  a meno di un addendo
a meno di un addendo
- ... analiticamente6
- vedi l'appendice
![]() ad uno stato
ad uno stato ![]() il punto
si sposta:
il punto
si sposta:
![]() è la media statistica (o
di ensemble) dei valori di
è la media statistica (o
di ensemble) dei valori di ![]() corrispondenti a un certo microstato
corrispondenti a un certo microstato
![]() :
:
![]() e di calcolare il corrispondente
e di calcolare il corrispondente ![]() , possiamo calcolare
, possiamo calcolare
![]() .
.
![\includegraphics[%
width=0.5\textwidth]{pianoEV.eps}](img15.png)
![\includegraphics[%
width=1\textwidth,
keepaspectratio]{chand-3-2.ps}](img48.png)
![\includegraphics[%
width=1\textwidth]{chand-3-3.ps}](img55.png)
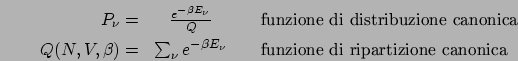
![\includegraphics[%
width=0.4\paperwidth,
keepaspectratio,
angle=2]{Sel-2.eps}](img81.png)
![\includegraphics[%
width=0.4\paperwidth,
keepaspectratio,
angle=2]{Sel-3.eps}](img82.png)
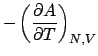
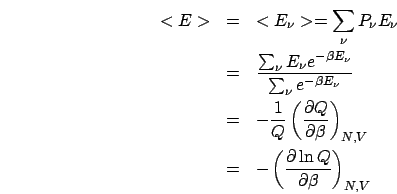

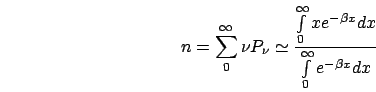
![\begin{eqnarray*}
\int\limits _{0}^{\infty}xe^{-\beta x}dx & = & \left[-\frac{e^...
...t[-\frac{e^{-\beta x}}{\beta}\right]_{0}^{\infty}=\frac{1}{\beta}\end{eqnarray*}](img106.png)