Next: Serial generalized ensemble simulations Up: The Hamiltonian Replica Exchange Previous: Hamiltonian REM Contents Index
As recently shown by Shirts and Chodera[107], all the
configurations produced by a REM simulation of ![]() replicas, each
characterized by a distribution function
replicas, each
characterized by a distribution function ![]() , can be effectively
used to obtain equilibrium averages for any target distribution
, can be effectively
used to obtain equilibrium averages for any target distribution
![]() , using the so-called Multistate Bennett Acceptance Ratio
(MBAR) estimator, which is illustrated in the following.
, using the so-called Multistate Bennett Acceptance Ratio
(MBAR) estimator, which is illustrated in the following.
In the ORAC REM implementation, the most general distribution
function for replica ![]() is given by Eq. 5.15. Given that
for each replica
is given by Eq. 5.15. Given that
for each replica ![]() one has saved
one has saved ![]() configurations of the kind
configurations of the kind
![]() , it can be easily shown that
, it can be easily shown that
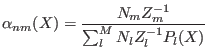 |
(5.25) |
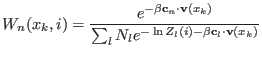 |
(5.28) |
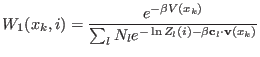 |
(5.32) |
In summary, using the configurational energies from all ![]() replicas,
we first solve iteratively the system 5.26 for all
replicas,
we first solve iteratively the system 5.26 for all ![]() (except for a multiplicative factor), with
(except for a multiplicative factor), with
![]() . In doing this, the weights
. In doing this, the weights ![]() (including
(including ![]() ) are also
determined. Finally configurational averages at, e.g., the target
distribution can be determined using all the REMD configurations
by means of Eq. 5.31.
) are also
determined. Finally configurational averages at, e.g., the target
distribution can be determined using all the REMD configurations
by means of Eq. 5.31.
procacci 2021-12-29